Overlapping Community Detection based on Network Decomposition

Abstract

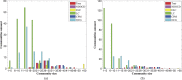
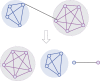
Community detection in complex network has become a vital step to understand the structure and dynamics of networks in various fields. However, traditional node clustering and relatively new proposed link clustering methods have inherent drawbacks to discover overlapping communities. Node clustering is inadequate to capture the pervasive overlaps, while link clustering is often criticized due to the high computational cost and ambiguous definition of communities. So, overlapping community detection is still a formidable challenge. In this work, we propose a new overlapping community detection algorithm based on network decomposition, called NDOCD. Specifically, NDOCD iteratively splits the network by removing all links in derived link communities, which are identified by utilizing node clustering technique. The network decomposition contributes to reducing the computation time and noise link elimination conduces to improving the quality of obtained communities. Besides, we employ node clustering technique rather than link similarity measure to discover link communities, thus NDOCD avoids an ambiguous definition of community and becomes less time-consuming. We test our approach on both synthetic and real-world networks. Results demonstrate the superior performance of our approach both in computation time and accuracy compared to state-of-the-art algorithms.

Figure 1. Comparison of computation time of different algorithms on synthetic networks with different sizes.

Plots show runtime (s) for networks with n = 100 ~ 1000, k = 10, k_max = 50, u = 0.1, τ₁ = 2, τ₂ = 1, c_max = 50, c_min = 10, o_m = 2, o_n/n = 10%.

Figure 2. The effects of mixing parameter u and network size n on synthetic networks.

(a) EQ for networks with n = 500, k = 25, k_max = 50, u = 0.1 ~ 0.6, τ₁ = 2, τ₂ = 1, c_max = 50, c_min = 10, o_m = 2, o_n/n = 10%, (b) ENMI for networks with n = 500, k = 25, k_max = 50, u = 0.1 ~ 0.6, τ₁ = 2, τ₂ = 1, c_max = 50, c_min = 10, o_m = 2, o_n/n = 10%, (c) EQ for networks with n = 100 ~ 1000, k = 25, k_max = 50, u = 0.1, τ₁ = 2, τ₂ = 1, c_max = 50, c_min = 10, o_m = 2, o_n/n = 10%, (d) ENMI for networks with n = 100 ~ 1000, k = 25, k_max = 50, u = 0.1, τ₁ = 2, τ₂ = 1, c_max = 50, c_min = 10, o_m = 2, o_n/n = 10%.

Figure 3. The effects of overlapping diversity o_m and overlapping density o_n/n on synthetic networks.

(a) EQ for networks with n = 500, k = 25, k_max = 50, u = 0.4, τ₁ = 2, τ₂ = 1, c_max = 50, c_min = 10, o_m = 2 ~ 8, o_n/n = 10%, (b) ENMI for networks with n = 500, k = 25, k_max = 50, u = 0.4, τ₁ = 2, τ₂ = 1, c_max = 50, c_min = 10, o_m = 2 ~ 8, o_n/n = 10%, (c) EQ for networks with n = 500, k = 25, k_max = 50, u = 0.4, τ₁ = 2, τ₂ = 1, c_max = 50, c_min = 10, o_m = 2, o_n/n = 10% ~ 60%, (d) ENMI for networks with n = 500, k = 25, k_max = 50, u = 0.4, τ₁ = 2, τ₂ = 1, c_max = 50, c_min = 10, o_m = 2, o_n/n = 10% ~ 60%.

Figure 4. Histogram of the detected community sizes on LFR benchmark.

(a) Comparison on networks with n = 500, k = 25, k_max = 50, u = 0.1, τ₁ = 2, τ₂ = 1, c_max = 50, c_min = 10, o_m = 2, o_n/n = 10%, (b) Comparison on networks with n = 500, k = 25, k_max = 50, u = 0.4, τ₁ = 2, τ₂ = 1, c_max = 50, c_min = 10, o_m = 2, o_n/n = 10%.

Figure 5. Precision, Recall and F-measure values for PPI-D1, PPI-D2 and Y2H.

(a) Precision values for PPI-D1, PPI-D2 and Y2H, (b) Recall values for PPI-D1, PPI-D2 and Y2H, (c) F-measure values for PPI-D1, PPI-D2 and Y2H.

Figure 6. Visualization of reference and predicted complexes in PPI-D1 for NDOCD, LC and OCG.

(a) Visualization of reference complexes, (b) Visualization of predicted complexes for NDOCD, (c) Visualization of predicted complexes for LC, (d) Visualization of predicted complexes for OCG.

Figure 7. An illustration of our main idea.

(a) Network decomposition procedure of our method, (b) Result of our method.

Figure 8. An example of bridge edge in a network.

The black line represents the bridge edge in the network.