Origins of the brain networks for advanced mathematics in expert mathematicians

Abstract

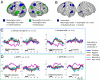
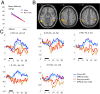
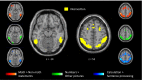
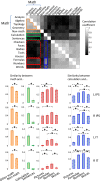
The origins of human abilities for mathematics are debated: Some theories suggest that they are founded upon evolutionarily ancient brain circuits for number and space and others that they are grounded in language competence. To evaluate what brain systems underlie higher mathematics, we scanned professional mathematicians and mathematically naive subjects of equal academic standing as they evaluated the truth of advanced mathematical and nonmathematical statements. In professional mathematicians only, mathematical statements, whether in algebra, analysis, topology or geometry, activated a reproducible set of bilateral frontal, Intraparietal, and ventrolateral temporal regions. Crucially, these activations spared areas related to language and to general-knowledge semantics. Rather, mathematical judgments were related to an amplification of brain activity at sites that are activated by numbers and formulas in nonmathematicians, with a corresponding reduction in nearby face responses. The evidence suggests that high-level mathematical expertise and basic number sense share common roots in a nonlinguistic brain circuit.

Keywords: functional MRI; mathematical cognition; semantic judgment.

Fig. 1.

Main paradigm and behavioral results. (A) On each trial, subjects listened to a spoken statement and, 4 s later, classified it as true, false, or meaningless. (B) Performance in this task (% correct). (C and D) Mean d′ values for discrimination of meaningful versus meaningless statements (C) and, within meaningful statements, of true versus false statements (D). *P < 0.05 (Student t tests). Error bars represent one SEM.

Fig. 2.

Distinct brain areas for mathematical expertise and for general semantic knowledge. (A) Whole-brain view of areas activated during reflection on mathematical statements (blue) versus general knowledge (green). In this figure and all subsequent figures, brain maps are thresholded at voxel P < 0.001, cluster P < 0.05 corrected for multiple comparisons across the brain volume. (B) Mathematical expertise effect: Interaction indicating a greater difference between meaningful math and nonmath statements in mathematicians than in controls. (C and D) Average fMRI signals in representative areas responsive to math (C) and to nonmath (D) (see SI Appendix, Fig. S1 for additional areas). Black rectangles indicate sentence presentation.

Fig. 3.

Variation in brain activation across mathematical problems. (A) Cortical sites where responses were common (red) or different (yellow) between analysis, algebra, topology, and geometry. The commonalities of the four mathematical domains were assessed by the intersection of activation maps for the contrasts analysis > nonmath, algebra > nonmath, topology > nonmath, and geometry > nonmath (each P < 0.001). Differences in cortical responses across mathematical domains were evaluated by an F-test at the whole-brain level (voxel P < 0.001, cluster P < 0.05 corrected). Bar plots show the activation for each mathematical domain at the principal peaks of three main regions identified in the latter F-contrast (R posterior parietal, L and R infero-temporal). (B) Cortical sites that showed a positive correlation between activation during math reflection and subjective imageability ratings within the meaningful statements in mathematicians.

Fig. 4.

Math and nonmath semantic effects. (A) Whole-brain view of semantic effects (meaningful > meaningless) for math statements in professional mathematicians (blue) and for nonmath statements in both groups (green). (B) Mathematical expertise effect: Interaction indicating a large difference between meaningful and meaningless math statements in mathematicians than in controls. (C and D) Average fMRI signals in representative areas responsive to math (C) and to nonmath (D) (see SI Appendix, Figs. S3 and S6 for additional areas).

Fig. 5.

Control for task difficulty. For each subject, math and nonmath statements were sorted into two levels of difficulty (easy versus difficult) depending on whether their subjective rating was below or above the subject’s mean. (A) Mean difficulty ratings for easy and difficult math and nonmath statements. The results indicate that activation is organized according to domain (math versus nonmath) rather than difficulty. (B) Axial slices showing the principal regions activated in the contrast “easy math > difficult nonmath” in mathematicians across all meaningful problems (voxel P < 0.001, cluster P < 0.05 corrected). This contrast revealed virtually the same sites as the ones that were activated for the standard math > nonmath contrast. (C) Plots report the temporal profile of activation at the principal peaks identified in the contrast of math > nonmath in mathematicians (same coordinates as SI Appendix, Fig. S1).

Fig. 6.

Overlap of the mathematical expertise network with areas involved in number recognition and arithmetic. Red, contrast of math versus nonmath statements in mathematicians; green, contrast of Arabic numerals versus all other visual stimuli in both mathematicians and controls; blue, contrast of single-digit calculation versus sentence processing in the localizer run, again in both groups; yellow, intersection of those three activation maps (each at P < 0.001).

Fig. 7.

Representational similarity analysis. (Top) Sample similarity matrix in left infero-temporal cortex showing the mean, across subjects, of the correlation between the spatial activation patterns evoked by the 15 experimental conditions of the whole experiment: four domains of math plus nonmath presented in auditory runs, calculation and spoken and written sentences from the localizer, and all pictures and symbols tested in visual runs. (Bottom) Mean correlation coefficients are shown in representative regions of interest of the math network. Colors indicate the provenance of the data in the similarity matrix. ROIs (left and right intraparietal sulci and infero-temporal cortices) were defined using a calculation localizer in a different group of subjects. *P < 0.05 (Student t tests). Error bars represent one SEM.

Fig. 8.

Effects of mathematical expertise on the ventral visual pathway. (A) Mosaic of preferences for different visual categories in ventral visual cortex. Slices show the activation for the contrast of a given category (represented by a specific color) minus all others. (B and C) A whole-brain search for larger responses in mathematicians than in controls revealed an effect for formulas in left ventral occipito-temporal cortex (B) and for tools in left lateral occipital cortex (C). Plots show the activation to each category relative to rest at the selected peak for mathematicians and controls. (D) A whole-brain search for smaller responses in mathematicians than in controls revealed an effect for faces in the right fusiform face area (FFA). (E) Slices showing the bilateral visual number form areas (VNFAs) in mathematicians and in controls, assessed by the contrast of numbers minus all other categories. At the peak of the left VNFA, a larger activation was found in mathematicians relative to controls for both numbers and formulas.