Tracking Resilience to Infections by Mapping Disease Space
- PMID: 27088359
- PMCID: PMC4835107
- DOI: 10.1371/journal.pbio.1002436
Tracking Resilience to Infections by Mapping Disease Space
Erratum in
-
Correction: Tracking Resilience to Infections by Mapping Disease Space.PLoS Biol. 2016 Jun 8;14(6):e1002494. doi: 10.1371/journal.pbio.1002494. eCollection 2016 Jun. PLoS Biol. 2016. PMID: 27276110 Free PMC article.
Abstract
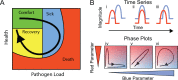
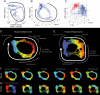
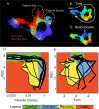
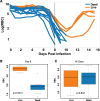
Infected hosts differ in their responses to pathogens; some hosts are resilient and recover their original health, whereas others follow a divergent path and die. To quantitate these differences, we propose mapping the routes infected individuals take through "disease space." We find that when plotting physiological parameters against each other, many pairs have hysteretic relationships that identify the current location of the host and predict the future route of the infection. These maps can readily be constructed from experimental longitudinal data, and we provide two methods to generate the maps from the cross-sectional data that is commonly gathered in field trials. We hypothesize that resilient hosts tend to take small loops through disease space, whereas nonresilient individuals take large loops. We support this hypothesis with experimental data in mice infected with Plasmodium chabaudi, finding that dying mice trace a large arc in red blood cells (RBCs) by reticulocyte space as compared to surviving mice. We find that human malaria patients who are heterozygous for sickle cell hemoglobin occupy a small area of RBCs by reticulocyte space, suggesting this approach can be used to distinguish resilience in human populations. This technique should be broadly useful in describing the in-host dynamics of infections in both model hosts and patients at both population and individual levels.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures



References
-
- Raberg l, Sim D, Read AF. Disentangling genetic variation for resistance and tolerance to infectious diseases in animals. Science. 2007;318:812–4. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

