The noisy voter model on complex networks
- PMID: 27094773
- PMCID: PMC4837380
- DOI: 10.1038/srep24775
The noisy voter model on complex networks
Abstract
We propose a new analytical method to study stochastic, binary-state models on complex networks. Moving beyond the usual mean-field theories, this alternative approach is based on the introduction of an annealed approximation for uncorrelated networks, allowing to deal with the network structure as parametric heterogeneity. As an illustration, we study the noisy voter model, a modification of the original voter model including random changes of state. The proposed method is able to unfold the dependence of the model not only on the mean degree (the mean-field prediction) but also on more complex averages over the degree distribution. In particular, we find that the degree heterogeneity--variance of the underlying degree distribution--has a strong influence on the location of the critical point of a noise-induced, finite-size transition occurring in the model, on the local ordering of the system, and on the functional form of its temporal correlations. Finally, we show how this latter point opens the possibility of inferring the degree heterogeneity of the underlying network by observing only the aggregate behavior of the system as a whole, an issue of interest for systems where only macroscopic, population level variables can be measured.
Figures
 .
.
 .
.
 .
.
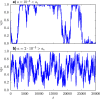
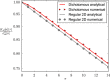
 : Erdös-Rényi random network, Barabási-Albert scale-free network and dichotomous network). Circles with error bars: Numerical results (averages over 20 networks, 10 realizations per network and 50000 time steps per realization). Solid line and squares: Analytical results [see equation (14)]. Dotted line: asymptotic approximation for small a [see equation (16)]. Dash-dotted line: asymptotic approximation for large a [see equation (17)]. Dashed line: Mean-field approximation (see42). The interaction parameter is fixed as h = 1, the system size as N = 2500 and the mean degree as
: Erdös-Rényi random network, Barabási-Albert scale-free network and dichotomous network). Circles with error bars: Numerical results (averages over 20 networks, 10 realizations per network and 50000 time steps per realization). Solid line and squares: Analytical results [see equation (14)]. Dotted line: asymptotic approximation for small a [see equation (16)]. Dash-dotted line: asymptotic approximation for large a [see equation (17)]. Dashed line: Mean-field approximation (see42). The interaction parameter is fixed as h = 1, the system size as N = 2500 and the mean degree as  .
.
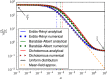
 : Erdös-Rényi random network, Barabási-Albert scale-free network and dichotomous network). Symbols: Numerical results (averages over 20 networks, 10 realizations per network and 50000 time steps per realization). Solid line: Analytical results [see equation (18)]. Dashed line: Mean-field approximation (see4244). The interaction parameter is fixed as h = 1, the system size as N = 2500 and the mean degree as
: Erdös-Rényi random network, Barabási-Albert scale-free network and dichotomous network). Symbols: Numerical results (averages over 20 networks, 10 realizations per network and 50000 time steps per realization). Solid line: Analytical results [see equation (18)]. Dashed line: Mean-field approximation (see4244). The interaction parameter is fixed as h = 1, the system size as N = 2500 and the mean degree as  .
.
 .
.
 .
.
 .
.Similar articles
-
Analytical and numerical study of the non-linear noisy voter model on complex networks.Chaos. 2018 Jul;28(7):075516. doi: 10.1063/1.5030112. Chaos. 2018. PMID: 30070524
-
Zealots in the mean-field noisy voter model.Phys Rev E. 2018 Jan;97(1-1):012310. doi: 10.1103/PhysRevE.97.012310. Phys Rev E. 2018. PMID: 29448335
-
Pair approximation for the q-voter model with independence on complex networks.Phys Rev E. 2017 Jan;95(1-1):012307. doi: 10.1103/PhysRevE.95.012307. Epub 2017 Jan 10. Phys Rev E. 2017. PMID: 28208483
-
Voter model dynamics in complex networks: Role of dimensionality, disorder, and degree distribution.Phys Rev E Stat Nonlin Soft Matter Phys. 2005 Sep;72(3 Pt 2):036132. doi: 10.1103/PhysRevE.72.036132. Epub 2005 Sep 30. Phys Rev E Stat Nonlin Soft Matter Phys. 2005. PMID: 16241540
-
Pair approximation for the noisy threshold q-voter model.Phys Rev E. 2020 May;101(5-1):052131. doi: 10.1103/PhysRevE.101.052131. Phys Rev E. 2020. PMID: 32575340
Cited by
-
Conformity in numbers-Does criticality in social responses exist?PLoS One. 2018 Dec 27;13(12):e0209620. doi: 10.1371/journal.pone.0209620. eCollection 2018. PLoS One. 2018. PMID: 30589873 Free PMC article.
-
Shadowing and shielding: Effective heuristics for continuous influence maximisation in the voting dynamics.PLoS One. 2021 Jun 18;16(6):e0252515. doi: 10.1371/journal.pone.0252515. eCollection 2021. PLoS One. 2021. PMID: 34143789 Free PMC article.
-
How social reinforcement learning can lead to metastable polarisation and the voter model.PLoS One. 2024 Dec 17;19(12):e0313951. doi: 10.1371/journal.pone.0313951. eCollection 2024. PLoS One. 2024. PMID: 39689073 Free PMC article.
-
Inference of monopartite networks from bipartite systems with different link types.Sci Rep. 2023 Jan 19;13(1):1072. doi: 10.1038/s41598-023-27744-8. Sci Rep. 2023. PMID: 36658171 Free PMC article.
-
Contrarian Voter Model under the Influence of an Oscillating Propaganda: Consensus, Bimodal Behavior and Stochastic Resonance.Entropy (Basel). 2022 Aug 17;24(8):1140. doi: 10.3390/e24081140. Entropy (Basel). 2022. PMID: 36010805 Free PMC article.
References
-
- Gunton J. D., San Miguel M. & Sahni P. S. The Dynamics of First Order Phase Transitions. In Phase Transitions Crit. Phenom. vol. 8, 269–466 (Academic Press, 1983).
-
- Marro J. & Dickman R. Nonequilibrium phase transitions in lattice models (Cambridge University Press, 1999).
-
- Clifford P. & Sudbury A. A model for spatial conflict. Biometrika 60, 581–588 (1973).
-
- Crawley M. J. & May R. M. Population dynamics and plant community structure: Competition between annuals and perennials. J. Theor. Biol. 125, 475–489 (1987).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

