Learning Biomarker Models for Progression Estimation of Alzheimer's Disease

Abstract

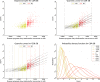
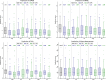
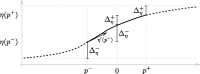
Being able to estimate a patient's progress in the course of Alzheimer's disease and predicting future progression based on a number of observed biomarker values is of great interest for patients, clinicians and researchers alike. In this work, an approach for disease progress estimation is presented. Based on a set of subjects that convert to a more severe disease stage during the study, models that describe typical trajectories of biomarker values in the course of disease are learned using quantile regression. A novel probabilistic method is then derived to estimate the current disease progress as well as the rate of progression of an individual by fitting acquired biomarkers to the models. A particular strength of the method is its ability to naturally handle missing data. This means, it is applicable even if individual biomarker measurements are missing for a subject without requiring a retraining of the model. The functionality of the presented method is demonstrated using synthetic and--employing cognitive scores and image-based biomarkers--real data from the ADNI study. Further, three possible applications for progress estimation are demonstrated to underline the versatility of the approach: classification, construction of a spatio-temporal disease progression atlas and prediction of future disease progression.

Fig 1. Illustration of the model training process on the example of the CDR-SB cognitive score.

(A) First, sample points are temporally aligned according to the point on conversion. The colours indicate MCI (yellow) or AD (red) diagnosis. (B) The progression model is then estimated using quantile regression. The quantile functions $y_q^b\left(p\right)$ with q ∈ {0.1, 0.25, 0.5, 0.75, 0.9} are visualised. (C) To increase the domain P, the model is then extrapolated. For each solid vertical line, the corresponding PDF is given in Fig 1D. (D) Illustration of the corresponding density functions f_Y^b (y|p), that indicate the probability of values y at given progresses p.

Fig 2. Illustration of the quantile functions of the synthetic models in blue.

In grey, models reconstructed from n_smp = 1000 random samples are shown.

Fig 3. Illustration of 100 random samples generated using uniform (left), triangular (center) and longitudinal (right) sampling.

The underlying model ${\tilde{\mathcal{M}}}^{\text{CDR-SB}}$ is shown in blue.

Fig 4. To measure the influence of the data pool on the model training, the sensitivity of quantile regression using VGAMs to different properties of the sampling set is analysed.

The graphs show the mean reconstruction error after 100 cycles of random sample generation and model training. The numbers above the boxes indicate the median error. (A) Sensitivity to the number of samples. (B) Sensitivity to the sampling strategy. (C) Robustness against temporal misalignment. (D) Sensitivity to different progression rates.

Fig 5. To illustrate the functionality of progress estimation for synthetic data, the mean estimation errors are computed based on a set of n_test = 100 randomly generated test samples.

The figures show the mean errors for n_runs = 100 runs of the experiments. The models correspond to the models analysed in Fig 4B. (A) Sensitivity to the sampling strategy. (B) Influence of additional data from more visits and multiple biomarkers.

Fig 6. Examples for progression models of several biomarkers learned based on the ADNI data base.

Visualised biomarkers are: Mini—mental State Examination (MMSE), the Alzheimer’s Disease Assessment Scale, 2013 (ADAS13), the Clinical Dementia Rating—Sum of Boxes (CDR-SB), the Functional Activities Questionnaire (FAQ), volumes of right hippocampus, amygdala and lateral ventricle, as well as the first and sixth manifold coordinates D1 and D6. In blue, models generated using the approach of Donohue et al. are shown for comparison [22].

Fig 7. Visualisation of the disease progress (DP) estimated with different biomarkers.

The x-axes show the disease progress in days before/after the conversion to AD. In the three columns, data from one, two and three visits is employed. The rows show results based on the different biomarker sets. The red bars indicate the median and 25th/75th percentile of the estimated DPS.

Fig 8. The generated 4D atlas depicting the the progression of Alzheimer’s disease, disentangled from the normal ageing of the subjects.

Fig 9. Concept of naive (left), DP- (center) and DP/DPR-based (right) prediction of biomarker values.

Fig 10. Illustration of observed (filled circles) and predicted (outlined circles) biomarker values for six randomly picked and representative subjects.

The slope of the naive linear prediction approach is visualised with a dashed line with $y_s^b\left(t\right)$ at the end. In a solid line, the quantile curve ${\overline{q}}_s$ is shown. The fitted progression model is shown in light grey.

Fig 11. Results for the prediction of future biomarker values for four different biomarkers (tree cognitive scores and the hippocampal volume).

The prediction of the value at m36 is based on bl, m12 and m24 visits, using the ADNI data. Bold median values indicate a statistically significant improvement over the naive approach (p < 0.01).

Fig 12. Illustration of the model extrapolation approach.