The implications of small stem cell niche sizes and the distribution of fitness effects of new mutations in aging and tumorigenesis
- PMID: 27099622
- PMCID: PMC4831459
- DOI: 10.1111/eva.12361
The implications of small stem cell niche sizes and the distribution of fitness effects of new mutations in aging and tumorigenesis
Abstract
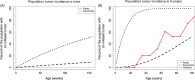
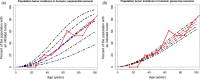
Somatic tissue evolves over a vertebrate's lifetime due to the accumulation of mutations in stem cell populations. Mutations may alter cellular fitness and contribute to tumorigenesis or aging. The distribution of mutational effects within somatic cells is not known. Given the unique regulatory regime of somatic cell division, we hypothesize that mutational effects in somatic tissue fall into a different framework than whole organisms; one in which there are more mutations of large effect. Through simulation analysis, we investigate the fit of tumor incidence curves generated using exponential and power-law distributions of fitness effects (DFE) to known tumorigenesis incidence. Modeling considerations include the architecture of stem cell populations, that is, a large number of very small populations, and mutations that do and do not fix neutrally in the stem cell niche. We find that the typically quantified DFE in whole organisms is sufficient to explain tumorigenesis incidence. Further, deleterious mutations are predicted to accumulate via genetic drift, resulting in reduced tissue maintenance. Thus, despite there being a large number of stem cells throughout the intestine, its compartmental architecture leads to the accumulation of deleterious mutations and significant aging, making the intestinal stem cell niche a prime example of Muller's Ratchet.
Keywords: aging; biomedicine; evolutionary theory; fitness; population genetics‐theoretical; stem cells; tumorigenesis.
Figures




References
-
- Barker, N. 2014. Adult intestinal stem cells: critical drivers of epithelial homeostasis and regeneration. Nature Reviews Molecular Cell Biology 15:19–33. - PubMed
-
- Bozic, I. , Antal T., Ohtsuki H., Carter H., Kim D., Chen S., Karchin R., Kinzler K. W., Vogelstein B., and Nowak M. A. 2010. Accumulation of driver and passenger mutations during tumor progression. Proceedings of the National Academy of Sciences of the United States of America 107:18545–18550. - PMC - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources

