First-order patterning transitions on a sphere as a route to cell morphology
- PMID: 27102872
- PMCID: PMC4868417
- DOI: 10.1073/pnas.1600296113
First-order patterning transitions on a sphere as a route to cell morphology
Abstract
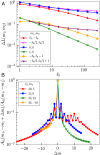
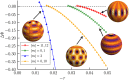
We propose a general theory for surface patterning in many different biological systems, including mite and insect cuticles, pollen grains, fungal spores, and insect eggs. The patterns of interest are often intricate and diverse, yet an individual pattern is robustly reproducible by a single species and a similar set of developmental stages produces a variety of patterns. We argue that the pattern diversity and reproducibility may be explained by interpreting the pattern development as a first-order phase transition to a spatially modulated phase. Brazovskii showed that for such transitions on a flat, infinite sheet, the patterns are uniform striped or hexagonal. Biological objects, however, have finite extent and offer different topologies, such as the spherical surfaces of pollen grains. We consider Brazovskii transitions on spheres and show that the patterns have a richer phenomenology than simple stripes or hexagons. We calculate the free energy difference between the unpatterned state and the many possible patterned phases, taking into account fluctuations and the system's finite size. The proliferation of variety on a sphere may be understood as a consequence of topology, which forces defects into perfectly ordered phases. The defects are then accommodated in different ways. We also argue that the first-order character of the transition is responsible for the reproducibility and robustness of the pattern formation.
Keywords: Brazovskii; pattern formation; phase transitions; pollen.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

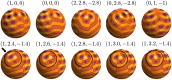
References
-
- Locke M. 1998. Epidermis. Microscopic Anatomy of Invertebrates, eds Harrison FW, Locke M (Wiley-Liss, New York), Vol 11A, pp 75–138.
-
- Alberti G, Coons LB. 1999. Acari: Mites. Microscopic Anatomy of Invertebrates, eds Harrison FW, Foelix RF (Wiley-Liss, New York), Vol 8C, pp 515–1265.
-
- Ariizumi T, Toriyama K. Genetic regulation of sporopollenin synthesis and pollen exine development. Annu Rev Plant Biol. 2011;62:437–460. - PubMed
-
- Crowe JH. Studies on acarine cuticles. III. Cuticular ridges in the citrus red mite. Trans Am Microsc Soc. 1975;94(1):98–108.
-
- De Almeida DN, Da Silva OR, Brazil BG, Soares MJ. Patterns of exochorion ornaments on eggs of seven South American species of Lutzomyia sand flies (Diptera: Psychodidae) J Med Entomol. 2004;41(5):819–825. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

