Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2016 Apr 28;11(4):e0154191.
doi: 10.1371/journal.pone.0154191. eCollection 2016.

Lagrange Interpolation Learning Particle Swarm Optimization

Zhang Kai  1 , Song Jinchun  1 , Ni Ke  1 , Li Song  1
Affiliations

Lagrange Interpolation Learning Particle Swarm Optimization

Zhang Kai et al. PLoS One. .

Abstract

In recent years, comprehensive learning particle swarm optimization (CLPSO) has attracted the attention of many scholars for using in solving multimodal problems, as it is excellent in preserving the particles' diversity and thus preventing premature convergence. However, CLPSO exhibits low solution accuracy. Aiming to address this issue, we proposed a novel algorithm called LILPSO. First, this algorithm introduced a Lagrange interpolation method to perform a local search for the global best point (gbest). Second, to gain a better exemplar, one gbest, another two particle's historical best points (pbest) are chosen to perform Lagrange interpolation, then to gain a new exemplar, which replaces the CLPSO's comparison method. The numerical experiments conducted on various functions demonstrate the superiority of this algorithm, and the two methods are proven to be efficient for accelerating the convergence without leading the particle to premature convergence.

PubMed Disclaimer

Conflict of interest statement

Competing Interests: The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. ForI ≠ 0, the different cases of the solution.
Fig 2
Fig 2. The flowchart of LSLI.
Fig 3
Fig 3. Selection of the exemplar dimensions for particle i.
(a)CLPSO (b)CLPSO-LIL.
Fig 4
Fig 4. The flowchart of LILPSO.
Fig 5
Fig 5. The comparison on convergence.
(a) Sphere (b) Rosenbrock (c) Noise Quadric (d) Penalized (e) Griewank (f) Schwefel.
See this image and copyright information in PMC

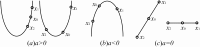
References

    1. Kennedy J., Eberhart R.C. Particle swarm optimization. in Proceedings of IEEE International Conference on Neural Networks, Piscataway, NJ, 1995; pp. 1942–1948.
    1. Kirkpatrick SC, Gelatt CD, Vecchi MP. Optimization by Simulated Annealing. Science. 1983;220(4598):671–80. 10.1126/science.220.4598.671 - DOI - PubMed
    1. Haddow BPC, Tufte G, editors. Goldberg D.E. Genetic Algorithms in Search, Optimization and Machine Learning Addison-Wesley Longman Publishing Co; In Proceedings of the 2000 Congress on Evolutionary Computation CEC00; 2010.
    1. Shi Y, Eberhart R C. A modified particle swarm optimizer. IEEE International Conference on Evolutionary Computation. Proceedings of the Piscataway, 1998; 1998b pp. 6973.
    1. By Y, Eberhart R, editors. 1998). “ Parameter selection in particle swarm optimization. Proceedings of the 7th Annual Conference on Evolutionary Programming; 2010.

LinkOut - more resources