Bottom-Up Colloidal Crystal Assembly with a Twist

Abstract

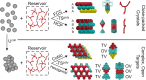
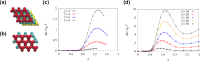
Globally ordered colloidal crystal lattices have broad utility in a wide range of optical and catalytic devices, for example, as photonic band gap materials. However, the self-assembly of stereospecific structures is often confounded by polymorphism. Small free-energy differences often characterize ensembles of different structures, making it difficult to produce a single morphology at will. Current techniques to handle this problem adopt one of two approaches: that of the "top-down" or "bottom-up" methodology, whereby structures are engineered starting from the largest or smallest relevant length scales, respectively. However, recently, a third approach for directing high fidelity assembly of colloidal crystals has been suggested which relies on the introduction of polymer cosolutes into the crystal phase [Mahynski, N.; Panagiotopoulos, A. Z.; Meng, D.; Kumar, S. K. Nat. Commun. 2014, 5, 4472]. By tuning the polymer's morphology to interact uniquely with the void symmetry of a single desired crystal, the entropy loss associated with polymer confinement has been shown to strongly bias the formation of that phase. However, previously, this approach has only been demonstrated in the limiting case of close-packed crystals. Here, we show how this approach may be generalized and extended to complex open crystals, illustrating the utility of this "structure-directing agent" paradigm in engineering the nanoscale structure of ordered colloidal materials. The high degree of transferability of this paradigm's basic principles between relatively simple crystals and more complex ones suggests that this represents a valuable addition to presently known self-assembly techniques.

Keywords: colloidal crystals; colloids; crystal polymorphism; polymers; self-assembly; tetrastack.

Figure 1

Schematic of the assembly paradigm in which a suspension of otherwise repulsive colloids is connected to a polymer reservoir where the polymer’s morphology is selected such that, when partitioned into the colloidal crystal at sufficient osmotic pressure, its morphology is commensurate with the local void symmetry found exclusively in one polymorph or another. (Top) This assembly route is purely based on the entropy loss of the polymer when adsorbed in a given crystal and has been previously shown to strongly bias the formation of one of the competing cubic and hexagonal polymorphic forms of close-packed crystals. (Bottom) By introducing thermal interactions between the colloids, it is plausible that a combination of colloidal energy and polymer entropy in the resulting crystal phase could be used to produce much more complex crystal morphologies in an intelligent fashion. In this work, we consider tetrastack crystals which are akin to close-packed ones in the sense that they have an identical topological distribution of octahedral voids (OV) and tetrahedral voids (TV) between different polymorphs.

Figure 2

Relative stability of tetrastack polymorphs in the presence of star polymers as predicted by Monte Carlo simulation. (a) Depiction of the cubic tetrastack crystal color-coded to illustrate the “ABC” stacking pattern. Each layer comprises tetrahedral sets of colloids packed in a hexagonal arrangement stacked out of the plane of the image in an alternating fashion, which is successively repeated to produce the macroscopic crystal. (b) Hexagonal polymorph is shown color-coded to illustrate the “ABAB” stacking pattern out of the plane. The visible gaps in the crystal correspond to octahedral voids which are stacked out of the plane shown. (c) Difference in the chemical potential of a given polymer confined in the two polymorphs, where Δμ = μ_cub – μ_hex, thus a positive Δμ corresponds to a lower free energy (higher stability) of the polymer when confined in the hexagonal polymorph. These simulations were performed with full monomeric resolution so that each point corresponds to a star, with a total of f arms, where the length of each arm, M_arm, is increased by one monomer. (d) Δμ/k_BT for coarse-grained high functionality star polymers as the overall size of the star, q, increases. Both the local maxima and minima in q are observed for all stars, as in the case of fully detailed simulations of low functionality stars in close-packed polymorphs.

Figure 3

Molecular dynamics simulation snapshots of triblock Janus particles. (a) Triblock Janus colloid modeled as a particle with two spherical polar patches (in blue). When two patches of different colloids are close to each other, the two colloids feel a net attraction whose magnitude depends on their relative distance and orientations (cf. Methods for the functional form of the potential). (b–d) Simulation snapshots where only crystalline colloids are shown (cf. Methods). Particles are color-coded according to the local environment: green (red) particles are in a cubic (hexagonal) local environment, while yellow particles are in a mixed environment. Patches are depicted in blue. (b) Snapshot of a pure colloidal system. The majority of the particles are in a crystallite formed by randomly stacking hexagonal and cubic layers. (c,d) Snapshot of simulations of a binary mixture of patchy particles and star polymers with f = 30 and q = 1.5. In (c), the relatively small star–star repulsion makes the system undergo a demixing transition, which pushes the colloids close to each other, forming a close-packed crystal. In (d), the same simulation was performed with charged star polymers, which experience a higher mutual repulsion that stabilizes open structures and biases the formation of the hexagonal tetrastack polymorph. As a consequence, nearly all crystalline particles are in a locally hexagonal environment.

Figure 4

Evolution of patchy particle crystals in molecular dynamics simulations. The color coding is the same as that in Figure 3. Coarse-grained star polymers with f = 30, q = 1.5 and a star–star repulsion increased by a factor of 6.5 due to electrostatic repulsion can be employed to anneal a cubic tetrastack crystallite into a hexagonal one. The snapshots (each of which refers to the point in the plot indicated by the accompanying letter) demonstrate how the annealing process takes place: the simulation starts from an initial configuration where all colloids are arranged on a cubic tetrastack lattice and the star polymers (which are shown only in the top-left picture) are randomly distributed throughout the sample. As the simulation proceeds, particles continuously detach from and reattach to the crystallite, slowly annealing into a hexagonal crystal. The black line in the plot shows the time dependence of the average bond order parameter ⟨q₄⟩, which starts from the cubic tetrastack value (green line, ⟨q₄⟩_c ≈ 0.513), decreases monotonically, and eventually plateaus to a value very close to the hexagonal tetrastack one (red line, ⟨q₄⟩_h ≈ 0.172). The small difference between the two values is due to a few (2–3) particles that are still in a mixed environment. The red (green) curve was obtained by simulating a hexagonal (cubic) crystallite with smaller stars (q = 0.75) which, as predicted by Monte Carlo calculations, do not affect the stability of either polymorph.