Efficient quantum walk on a quantum processor

Abstract

The random walk formalism is used across a wide range of applications, from modelling share prices to predicting population genetics. Likewise, quantum walks have shown much potential as a framework for developing new quantum algorithms. Here we present explicit efficient quantum circuits for implementing continuous-time quantum walks on the circulant class of graphs. These circuits allow us to sample from the output probability distributions of quantum walks on circulant graphs efficiently. We also show that solving the same sampling problem for arbitrary circulant quantum circuits is intractable for a classical computer, assuming conjectures from computational complexity theory. This is a new link between continuous-time quantum walks and computational complexity theory and it indicates a family of tasks that could ultimately demonstrate quantum supremacy over classical computers. As a proof of principle, we experimentally implement the proposed quantum circuit on an example circulant graph using a two-qubit photonics quantum processor.

Figure 1. Applications for generating the time-evolution state of circulant Hamiltonians.

(a) The SWAP test can be used to estimate the similarity of two evolution states of two similar circulant systems, or when one of the Hamiltonians is non-circulant but efficiently implementable. In brief, an ancillary qubit is entangled with the output states and of two compared processes according to . On measuring the ancillary qubit we obtain outcome ‘1' with probability —the probability of observing ‘1' indicates the similarity of dynamical behaviours of the two processes. See its complexity analysis in Supplementary Note 1. (b) Probability distributions are sampled by measuring the evolution state in a complete basis, such as the computational basis. (c) An example of the quantum circuit for implementing diagonal unitary operator D=exp(−itΛ), where the circulant Hamiltonian has 5 non-zero eigenvalues. The open and solid circles represent the control qubits as ‘if ' and ‘if ', respectively. , where is the corresponding eigenvalue.

Figure 2. The schematic diagram and set-up of experimental demonstration.

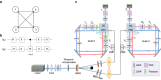
(a) The K₄ graph. (b) The quantum circuit for implementing CTQW on the K₄ graph. This can also be used to implement CTQW on the K₄ graph without self-loops, up to a global phase factor . H and X represent the Hadamard and Pauli-X gate, respectively. is a phase gate. (c) The experimental set-up for a reconfigurable two-qubit photonics quantum processor, consisting of a polarization-entangled photon source using paired type-I BiBO crystal in the sandwich configuration and displaced Sagnac interferometers. See further details in Methods.

Figure 3. Experimental results for simulating CTQWs on K₄.

(a,b) The experimental sampled probability distributions with ideal theoretical distributions overlaid, for CTQWs on K₄ graph with initial states and . The s.d. of each individual probability is also plotted, which is calculated by propagating error assuming Poissonian statistics. (c,d) The ideal theoretical and experimentally reconstructed density matrices for the states (corresponding to ρ₁) and (corresponding to ρ₂). Both of the real and imaginary parts of the density matrices are obtained through the maximum likelihood estimation technique, and is shown as Re(ρ) and Im(ρ), respectively. Further results are shown in Supplementary Table 1, Supplementary Fig. 2 and Supplementary Note 4.