Feed-Forward Propagation of Temporal and Rate Information between Cortical Populations during Coherent Activation in Engineered In Vitro Networks
- PMID: 27147977
- PMCID: PMC4840215
- DOI: 10.3389/fncir.2016.00032
Feed-Forward Propagation of Temporal and Rate Information between Cortical Populations during Coherent Activation in Engineered In Vitro Networks
Abstract
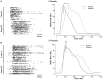
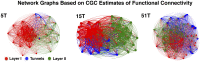
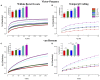
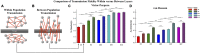
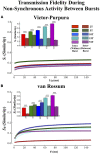
Transient propagation of information across neuronal assembles is thought to underlie many cognitive processes. However, the nature of the neural code that is embedded within these transmissions remains uncertain. Much of our understanding of how information is transmitted among these assemblies has been derived from computational models. While these models have been instrumental in understanding these processes they often make simplifying assumptions about the biophysical properties of neurons that may influence the nature and properties expressed. To address this issue we created an in vitro analog of a feed-forward network composed of two small populations (also referred to as assemblies or layers) of living dissociated rat cortical neurons. The populations were separated by, and communicated through, a microelectromechanical systems (MEMS) device containing a strip of microscale tunnels. Delayed culturing of one population in the first layer followed by the second a few days later induced the unidirectional growth of axons through the microtunnels resulting in a primarily feed-forward communication between these two small neural populations. In this study we systematically manipulated the number of tunnels that connected each layer and hence, the number of axons providing communication between those populations. We then assess the effect of reducing the number of tunnels has upon the properties of between-layer communication capacity and fidelity of neural transmission among spike trains transmitted across and within layers. We show evidence based on Victor-Purpura's and van Rossum's spike train similarity metrics supporting the presence of both rate and temporal information embedded within these transmissions whose fidelity increased during communication both between and within layers when the number of tunnels are increased. We also provide evidence reinforcing the role of synchronized activity upon transmission fidelity during the spontaneous synchronized network burst events that propagated between layers and highlight the potential applications of these MEMs devices as a tool for further investigation of structure and functional dynamics among neural populations.
Keywords: cortical networks; feed-forward networks; information transmission; multielectrode array; neural populations; neural transmission; neuronal assembly; synchrony.
Figures

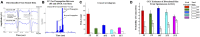
Similar articles
-
An in vitro method to manipulate the direction and functional strength between neural populations.Front Neural Circuits. 2015 Jul 14;9:32. doi: 10.3389/fncir.2015.00032. eCollection 2015. Front Neural Circuits. 2015. PMID: 26236198 Free PMC article. Review.
-
Network burst activity in hippocampal neuronal cultures: the role of synaptic and intrinsic currents.J Neurophysiol. 2016 Jun 1;115(6):3073-89. doi: 10.1152/jn.00995.2015. Epub 2016 Mar 16. J Neurophysiol. 2016. PMID: 26984425 Free PMC article.
-
Signal transfer within a cultured asymmetric cortical neuron circuit.J Neural Eng. 2015 Dec;12(6):066023. doi: 10.1088/1741-2560/12/6/066023. Epub 2015 Nov 3. J Neural Eng. 2015. PMID: 26529359
-
Deterministic neural dynamics transmitted through neural networks.Neural Netw. 2008 Aug;21(6):799-809. doi: 10.1016/j.neunet.2008.06.014. Epub 2008 Jun 28. Neural Netw. 2008. PMID: 18675536
-
Implications of synaptic biophysics for recurrent network dynamics and active memory.Neural Netw. 2009 Oct;22(8):1189-200. doi: 10.1016/j.neunet.2009.07.016. Epub 2009 Jul 21. Neural Netw. 2009. PMID: 19647396 Review.
Cited by
-
Microfluidics for Neuronal Cell and Circuit Engineering.Chem Rev. 2022 Sep 28;122(18):14842-14880. doi: 10.1021/acs.chemrev.2c00212. Epub 2022 Sep 7. Chem Rev. 2022. PMID: 36070858 Free PMC article. Review.
-
Coupling of in vitro Neocortical-Hippocampal Coculture Bursts Induces Different Spike Rhythms in Individual Networks.Front Neurosci. 2022 May 23;16:873664. doi: 10.3389/fnins.2022.873664. eCollection 2022. Front Neurosci. 2022. PMID: 35677356 Free PMC article.
-
Design of Cultured Neuron Networks in vitro with Predefined Connectivity Using Asymmetric Microfluidic Channels.Sci Rep. 2017 Nov 15;7(1):15625. doi: 10.1038/s41598-017-15506-2. Sci Rep. 2017. PMID: 29142321 Free PMC article.
-
Exploring Kainic Acid-Induced Alterations in Circular Tripartite Networks with Advanced Analysis Tools.eNeuro. 2024 Jul 30;11(7):ENEURO.0035-24.2024. doi: 10.1523/ENEURO.0035-24.2024. Print 2024 Jul. eNeuro. 2024. PMID: 39079743 Free PMC article.
-
Neural Circuits on a Chip.Micromachines (Basel). 2016 Sep 5;7(9):157. doi: 10.3390/mi7090157. Micromachines (Basel). 2016. PMID: 30404330 Free PMC article. Review.
References
-
- Abeles M., Bergman H., Margalit E., Vaadia E. (1993). Spatiotemporal firing patterns in the frontal cortex of behaving monkeys. J. Neurophysiol. 70, 1629–1638. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

