Pathogen Propagation Model with Superinfection in Vegetatively Propagated Plants on Lattice Space

Abstract

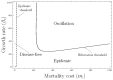
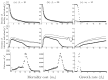
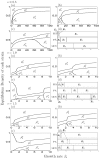
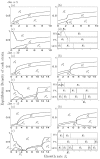
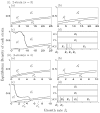
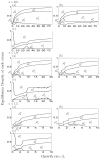
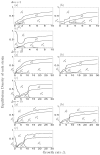
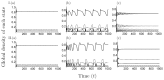
Many clonal plants have two reproductive patterns, seed propagation and vegetative propagation. By vegetative propagation, plants reproduce the genetically identical offspring with a low mortality, because resources are supplied from the other individuals through interconnected ramets at vegetative-propagated offspring. However, the ramets transport not only resources but also systemic pathogen. Pathogens evolve to establish and spread widely within the plant population. The superinfection, which is defined as the ability that an established pathogen spreads widely by infecting to already-infected individuals with other strains of a pathogen, is important to the evolution of pathogens. We examine the dynamics of plant reproduction and pathogen propagation considering spatial structure and the effect of superinfection on genetic diversity of pathogen by analysis of several models, 1-strain and multiple-strain models, on two-dimensional square lattice. In the analysis of 1-strain model, we derive equilibrium value by mean-field approximation and pair approximation, and its local stability by Routh-Hurwitz stability criterion. In the multiple-strain models, we analyze the dynamics by numerical simulation of mean-field approximation, pair approximation and Monte Carlo simulation. Through the analyses, we show the effect of parameter values to dynamics of models, such as transition of dominant strain of pathogen, competition between plants and pathogens and density of individuals. As a result, (i) The strain with intermediate cost becomes dominant when both superinfection rate and growth rate are low. (ii) The competition between plants and pathogens occurs in the phase of coexistence of various strains by pair approximation and Monte Carlo simulation. (iii) Too high growth rate leads to the decrease of plant population in all models. (iv) Pathogens are easy to maintain their genetic diversity with low superinfection rate. However, if they do not superinfect, the maintenance becomes difficult. (v) When growth rate of plant is low, individuals are very influenced by distant individuals.

Fig 1. Phase diagram of pair approximation showing the three regions of the equilibrium state.

In the epidemic region, plants and pathogens coexist and the equilibrium is stable. In the oscillation region, plants and pathogens coexist, but the equilibrium is unstable. Therefore, Hopf bifurcation occurs and oscillation is observed. The solid line indicates the bifurcation threshold, and the dashed line the epidemic threshold, respectively. In the disease-free region, pathogens become extinct because of the too low mortality cost.

Fig 2. Comparison of the simulation results from mean-field approximation (MA), pair approximation (PA) and Monte Carlo simulation (MCS), depending on mortality cost and growth rate; (a). β_S = 10, (b). β_S = 30, (c). m_I = 15.

(i) equilibrium density of healthy individuals (${\rho }_{\mathrm{S}}^{*}$) (ii) equilibrium density of infected individuals (${\rho }_{\mathrm{I}}^{*}$). The dots, solid line and dashed line indicate the results of MA, PA and MCS, respectively. These results show that when m_I is low, both approximation methods present similar trend to MCS, although these methods overestimate the equilibrium value. (iii) The variance among 100 trials in MCS. A high variance means the oscillatory solution is observed.

Fig 3. The equilibrium value of each state and transition of the equilibrium phase depending on the superinfection rate in the 2-strain model.

We set m₁ = 5 and Δm = 5. The I, II and III differ in the value of s (=0.5, 1.0, 1.5). (a)–(c) show the variation of the equilibrium density of each state (“0”, “S”, “I₁” and “I₂”. Σ_σ ρ_σ = 1) with growth rate in each simulation: (a) MA, (b) PA, (c) MCS. (d) shows the transition of the equilibrium phase with β_S in MA, PA, and MCS.

Fig 4. The equilibrium value of each strain and transition of the equilibrium phase depending on the difference of mortality cost in the 2-strain model.

We set m_I1 = 5 and Δm = 5 in all figures. The I, II and III differ in the value of s (=0.5, 1.0, 1.5). (a) MA, (b) PA, (c) MCS, (d) the transition of equilibrium phase.

Fig 5. The case of no superinfection (s = 0) in the 2-strain and 3-strain model by MA, PA and MCS.

We plotted the global density of each strain of the pathogen at the equilibrium state depending on β_S. The black circles and triangles indicate I₁ and I₂, respectively, and squares indicate I₃ in (b). The parameter values are (a) n = 3, m_I1 = 5, Δm = 10, (b) n = 4, m_I1 = 5, Δm = 5.

Fig 6. Time development in the 2-strain model.

We plotted the equilibrium value of the global density of each state. In all figures, we set s = 1.0 and Δm = 15. I. m_I1 = 5, II. m_I1 = 30 and (a) β_S = 10, (b) β_S = 15, (c) β_S = 25.

Fig 7. The equilibrium value of each strain depending on the superinfection rate in the 3-strain model.

We set m_I1 = 5 and Δm = 5 in all figures. The I, II and III differ in the value of s (=0.5, 1.0, 1.5). (a) MA, (b) PA, (c) MCS.

Fig 8. The equilibrium value of each strain depending on the difference in the mortality cost in the 3-strain model.

We set m_I1 = 5 and s = 1.5 in all figures. The I, II and III differ in the value of Δm (=5, 10, 15). (a) MA, (b) PA, (c) MCS.

Fig 9. Time development of global density of each state in the 3-strain model.

We plotted the equilibrium value of the global density of each state. We set the parameter values; I. s = 1.0, m_I1 = 10, Δm = 15, II. s = 1.5, m_I1 = 10, Δm = 20 and (a) β_S = 3, (b) β_S = 5, (c) β_S = 7. In the 3-strain model, the oscillatory solution was observed in a particular parameter range at the coexistence phase (panel(b)).

Fig 10. The equilibrium density distribution of strains in 10-strain model.

The left, center and right panels show the result in simulation by MA, PA and MCS, respectively. We set m_I1 = 5, Δm = 5 and other parameter values are: I. s = 0.5, β_S = 25, II. s = 1.0, β_S = 25, III. s = 1.5, β_S = 25, IV. s = 1.5, β_S = 5.

Fig 11. The equilibrium density distribution of strains in the 25-strain model.

The left, center and right panels show the result in simulation by MA, PA and MCS, respectively. We set m_I1 = 5, Δm = 5 and other parameter values are: I. s = 0.5, β_S = 5, II. s = 0.5, β_S = 25, III. s = 1.0, β_S = 25, IV. s = 1.5, β_S = 25.

Fig 12. Time development in the 25-strain model.

We plotted the equilibrium value of the global density of each state. In the all figures, we set m_I1 = 5, Δm = 5 and β_S = 5, and (a) s = 1.5, (b) s = 0.5.