Rigid proteins and softening of biological membranes-with application to HIV-induced cell membrane softening
- PMID: 27149877
- PMCID: PMC4858729
- DOI: 10.1038/srep25412
Rigid proteins and softening of biological membranes-with application to HIV-induced cell membrane softening
Abstract
A key step in the HIV-infection process is the fusion of the virion membrane with the target cell membrane and the concomitant transfer of the viral RNA. Experimental evidence suggests that the fusion is preceded by considerable elastic softening of the cell membranes due to the insertion of fusion peptide in the membrane. What are the mechanisms underpinning the elastic softening of the membrane upon peptide insertion? A broader question may be posed: insertion of rigid proteins in soft membranes ought to stiffen the membranes not soften them. However, experimental observations perplexingly appear to show that rigid proteins may either soften or harden membranes even though conventional wisdom only suggests stiffening. In this work, we argue that regarding proteins as merely non-specific rigid inclusions is flawed, and each protein has a unique mechanical signature dictated by its specific interfacial coupling to the surrounding membrane. Predicated on this hypothesis, we have carried out atomistic simulations to investigate peptide-membrane interactions. Together with a continuum model, we reconcile contrasting experimental data in the literature including the case of HIV-fusion peptide induced softening. We conclude that the structural rearrangements of the lipids around the inclusions cause the softening or stiffening of the biological membranes.
Figures





 and the inner boundary between peptide and membrane by ∂Ω. We use an homogenization approach to obtain the effective bending modulus of this protein-membrane system, represented by
and the inner boundary between peptide and membrane by ∂Ω. We use an homogenization approach to obtain the effective bending modulus of this protein-membrane system, represented by  .
.
 . The inner surface of the protein is represented by ∂Ω− and outer surface (which is towards the membrane) by ∂Ω+. The effective bending modulus of this protein membrane system is found by modifying the Helfrich Hamiltonian and taking into account the interface by introducing jump energies parametrized by k1 and k2.
. The inner surface of the protein is represented by ∂Ω− and outer surface (which is towards the membrane) by ∂Ω+. The effective bending modulus of this protein membrane system is found by modifying the Helfrich Hamiltonian and taking into account the interface by introducing jump energies parametrized by k1 and k2.
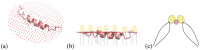

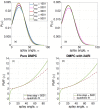
 where α are the angles between lipid-lipid pairs. A quadratic fit is performed to the PMF at small angles of α to evaluate Splay Modulus of the lipid monolayer.
where α are the angles between lipid-lipid pairs. A quadratic fit is performed to the PMF at small angles of α to evaluate Splay Modulus of the lipid monolayer.Similar articles
-
Ectodomain Pulling Combines with Fusion Peptide Inserting to Provide Cooperative Fusion for Influenza Virus and HIV.Int J Mol Sci. 2020 Jul 29;21(15):5411. doi: 10.3390/ijms21155411. Int J Mol Sci. 2020. PMID: 32751407 Free PMC article.
-
Role of the fusion peptide and membrane-proximal domain in HIV-1 envelope glycoprotein-mediated membrane fusion.Biochemistry. 2003 Dec 9;42(48):14150-8. doi: 10.1021/bi035154g. Biochemistry. 2003. PMID: 14640682
-
Revisiting the curvature-mediated interactions between proteins in biological membranes.Soft Matter. 2016 Nov 4;12(43):8907-8918. doi: 10.1039/c6sm01572g. Soft Matter. 2016. PMID: 27725970
-
Broad-spectrum antivirals against viral fusion.Nat Rev Microbiol. 2015 Jul;13(7):426-37. doi: 10.1038/nrmicro3475. Epub 2015 Jun 15. Nat Rev Microbiol. 2015. PMID: 26075364 Free PMC article. Review.
-
Remodeling of the Host Cell Plasma Membrane by HIV-1 Nef and Vpu: A Strategy to Ensure Viral Fitness and Persistence.Viruses. 2016 Mar 3;8(3):67. doi: 10.3390/v8030067. Viruses. 2016. PMID: 26950141 Free PMC article. Review.
Cited by
-
Thermodynamically reversible paths of the first fusion intermediate reveal an important role for membrane anchors of fusion proteins.Proc Natl Acad Sci U S A. 2019 Feb 12;116(7):2571-2576. doi: 10.1073/pnas.1818200116. Epub 2019 Jan 30. Proc Natl Acad Sci U S A. 2019. PMID: 30700547 Free PMC article.
-
Effect of gold nanoparticle incorporation into oil-swollen surfactant lamellar membranes.Struct Dyn. 2020 Dec 15;7(6):065102. doi: 10.1063/4.0000041. eCollection 2020 Nov. Struct Dyn. 2020. PMID: 33344674 Free PMC article.
-
Synergistic actions of v-SNARE transmembrane domains and membrane-curvature modifying lipids in neurotransmitter release.Elife. 2020 May 11;9:e55152. doi: 10.7554/eLife.55152. Elife. 2020. PMID: 32391794 Free PMC article.
-
Collective dynamics in lipid membranes containing transmembrane peptides.Soft Matter. 2021 Jun 16;17(23):5671-5681. doi: 10.1039/d1sm00314c. Soft Matter. 2021. PMID: 33942045 Free PMC article.
-
On the Coupling between Mechanical Properties and Electrostatics in Biological Membranes.Membranes (Basel). 2021 Jun 28;11(7):478. doi: 10.3390/membranes11070478. Membranes (Basel). 2021. PMID: 34203412 Free PMC article. Review.
References
-
- Phillips R., Kondev J., Theriot J. & Garcia H. Physical biology of the cell 1st edn (ed. Scholl S.) (Garland Science, 2008).
-
- Dimova R. Recent developments in the field of bending rigidity measurements on membranes. Adv. Colloid Interface Sci. 208, 225–234 (2014). - PubMed
-
- Bouvrais H. et al.. Softening of POPC membranes by magainin. Biophys. Chem. 137(1), 7–12 (2008). - PubMed
-
- Vitkova V., Meleard P., Pott T. & Bivas I. Alamethicin influence on the membrane bending elasticity. Eur. Biophys. J. 35(3), 281–286 (2006). - PubMed
-
- Hackl W., Seifert U. & Sackmann E. Effects of fully and partially solubilized amphiphiles on bilayer bending stiffness and temperature dependence of the effective tension of giant vesicles. J. Phys. II 7(8), 1141–1157 (1997).
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

