The Physics and Physical Chemistry of Molecular Machines
- PMID: 27149926
- PMCID: PMC5518708
- DOI: 10.1002/cphc.201600184
The Physics and Physical Chemistry of Molecular Machines
Abstract
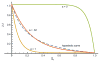
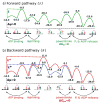
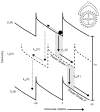
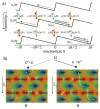
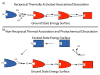
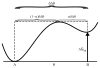
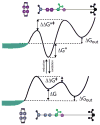
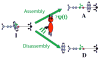
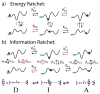
The concept of a "power stroke"-a free-energy releasing conformational change-appears in almost every textbook that deals with the molecular details of muscle, the flagellar rotor, and many other biomolecular machines. Here, it is shown by using the constraints of microscopic reversibility that the power stroke model is incorrect as an explanation of how chemical energy is used by a molecular machine to do mechanical work. Instead, chemically driven molecular machines operating under thermodynamic constraints imposed by the reactant and product concentrations in the bulk function as information ratchets in which the directionality and stopping torque or stopping force are controlled entirely by the gating of the chemical reaction that provides the fuel for the machine. The gating of the chemical free energy occurs through chemical state dependent conformational changes of the molecular machine that, in turn, are capable of generating directional mechanical motions. In strong contrast to this general conclusion for molecular machines driven by catalysis of a chemical reaction, a power stroke may be (and often is) an essential component for a molecular machine driven by external modulation of pH or redox potential or by light. This difference between optical and chemical driving properties arises from the fundamental symmetry difference between the physics of optical processes, governed by the Bose-Einstein relations, and the constraints of microscopic reversibility for thermally activated processes.
Keywords: Brownian motors; energy landscapes; information ratchet; microscopic reversibility; molecular machines.
© 2016 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim.
Figures



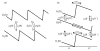




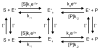

References
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

