Adaptive Multilevel Splitting Method for Molecular Dynamics Calculation of Benzamidine-Trypsin Dissociation Time
- PMID: 27159059
- PMCID: PMC5724379
- DOI: 10.1021/acs.jctc.6b00277
Adaptive Multilevel Splitting Method for Molecular Dynamics Calculation of Benzamidine-Trypsin Dissociation Time
Abstract
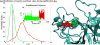
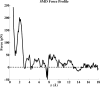
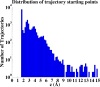
Adaptive multilevel splitting (AMS) is a rare event sampling method that requires minimal parameter tuning and allows unbiased sampling of transition pathways of a given rare event. Previous simulation studies have verified the efficiency and accuracy of AMS in the calculation of transition times for simple systems in both Monte Carlo and molecular dynamics (MD) simulations. Now, AMS is applied for the first time to an MD simulation of protein-ligand dissociation, representing a leap in complexity from the previous test cases. Of interest is the dissociation rate, which is typically too low to be accessible to conventional MD. The present study joins other recent efforts to develop advanced sampling techniques in MD to calculate dissociation rates, which are gaining importance in the pharmaceutical field as indicators of drug efficacy. The system investigated here, benzamidine bound to trypsin, is an example common to many of these efforts. The AMS estimate of the dissociation rate was found to be (2.6 ± 2.4) × 10(2) s(-1), which compares well with the experimental value.
Figures



Similar articles
-
Exploring the Ligand Binding/Unbinding Pathway by Selectively Enhanced Sampling of Ligand in a Protein-Ligand Complex.J Phys Chem B. 2019 Sep 26;123(38):7974-7983. doi: 10.1021/acs.jpcb.9b05226. Epub 2019 Sep 12. J Phys Chem B. 2019. PMID: 31478672
-
How Effectively Can Adaptive Sampling Methods Capture Spontaneous Ligand Binding?J Chem Theory Comput. 2019 Mar 12;15(3):2053-2063. doi: 10.1021/acs.jctc.8b00913. Epub 2019 Feb 4. J Chem Theory Comput. 2019. PMID: 30645108 Free PMC article.
-
Protein conformational plasticity and complex ligand-binding kinetics explored by atomistic simulations and Markov models.Nat Commun. 2015 Jul 2;6:7653. doi: 10.1038/ncomms8653. Nat Commun. 2015. PMID: 26134632 Free PMC article.
-
Advances in computational methods for ligand binding kinetics.Trends Biochem Sci. 2023 May;48(5):437-449. doi: 10.1016/j.tibs.2022.11.003. Epub 2022 Dec 22. Trends Biochem Sci. 2023. PMID: 36566088 Review.
-
Exploring biomolecular dynamics and interactions using advanced sampling methods.J Phys Condens Matter. 2015 Aug 19;27(32):323101. doi: 10.1088/0953-8984/27/32/323101. Epub 2015 Jul 21. J Phys Condens Matter. 2015. PMID: 26194626 Review.
Cited by
-
Quantitative Ranking of Ligand Binding Kinetics with a Multiscale Milestoning Simulation Approach.J Phys Chem Lett. 2018 Sep 6;9(17):4941-4948. doi: 10.1021/acs.jpclett.8b02047. Epub 2018 Aug 16. J Phys Chem Lett. 2018. PMID: 30070844 Free PMC article.
-
Mapping the Ligand Binding Landscape.Biophys J. 2018 Nov 6;115(9):1707-1719. doi: 10.1016/j.bpj.2018.09.021. Epub 2018 Sep 29. Biophys J. 2018. PMID: 30327139 Free PMC article.
-
How and when does an anticancer drug leave its binding site?Sci Adv. 2017 May 31;3(5):e1700014. doi: 10.1126/sciadv.1700014. eCollection 2017 May. Sci Adv. 2017. PMID: 28580424 Free PMC article.
-
Predicting ligand binding affinity using on- and off-rates for the SAMPL6 SAMPLing challenge.J Comput Aided Mol Des. 2018 Oct;32(10):1001-1012. doi: 10.1007/s10822-018-0149-3. Epub 2018 Aug 23. J Comput Aided Mol Des. 2018. PMID: 30141102 Free PMC article.
-
Rapid, accurate, precise and reproducible ligand-protein binding free energy prediction.Interface Focus. 2020 Dec 6;10(6):20200007. doi: 10.1098/rsfs.2020.0007. Epub 2020 Oct 16. Interface Focus. 2020. PMID: 33178418 Free PMC article. Review.
References
-
- Glynn PW, Iglehart DL. Management Sci. 1989;35:1367–1392.
-
- van Erp TS, Moroni D, Bolhuis PG. J Chem Phys. 2003;118:7762–7774.
-
- van Erp TS, Bolhuis PG. J Comp Phys. 2005;205:157–181.
-
- Allen RJ, Warren PB, ten Wolde PR. Phys Rev Lett. 2005;94:018104. - PubMed
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
