Antimicrobial combinations: Bliss independence and Loewe additivity derived from mechanistic multi-hit models

Abstract

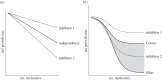
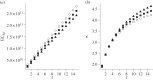
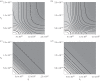
Antimicrobial peptides (AMPs) and antibiotics reduce the net growth rate of bacterial populations they target. It is relevant to understand if effects of multiple antimicrobials are synergistic or antagonistic, in particular for AMP responses, because naturally occurring responses involve multiple AMPs. There are several competing proposals describing how multiple types of antimicrobials add up when applied in combination, such as Loewe additivity or Bliss independence. These additivity terms are defined ad hoc from abstract principles explaining the supposed interaction between the antimicrobials. Here, we link these ad hoc combination terms to a mathematical model that represents the dynamics of antimicrobial molecules hitting targets on bacterial cells. In this multi-hit model, bacteria are killed when a certain number of targets are hit by antimicrobials. Using this bottom-up approach reveals that Bliss independence should be the model of choice if no interaction between antimicrobial molecules is expected. Loewe additivity, on the other hand, describes scenarios in which antimicrobials affect the same components of the cell, i.e. are not acting independently. While our approach idealizes the dynamics of antimicrobials, it provides a conceptual underpinning of the additivity terms. The choice of the additivity term is essential to determine synergy or antagonism of antimicrobials.This article is part of the themed issue 'Evolutionary ecology of arthropod antimicrobial peptides'.

Keywords: antagonism; antibiotics; antimicrobial peptide responses; mathematical modelling; pharmacodynamic function; synergy.

Figure 1.

The shape of the pharmacodynamic function determines the difference between predicted combination effects. Here, we show predicted effects for both Bliss independence and Loewe additivity (see §2) dependent on the number of inhibitor molecules. We plotted the combined effect for a 1 : 1 mixture of the two inhibitors, scaled by a factor 0.5 to adjust for the amount of inhibitors in combination. With this scaling, we are able to plot both the single effect curves and the combined effect curves using the same x-axis. (a) In the hypothetical case of linear pharmacodynamic functions describing single inhibitor effects of inhibitor 1 and 2, respectively, combined effects according to Bliss and Loewe are congruent (independence). Here, the effect in combination is equal to the sum of the two individual effects. The addition of the individual effects of inhibitor 1 and inhibitor 2 with n molecules each is equal to the effect of the combination of the inhibitors with 2n molecules. (b) For realistically sigmoid-shaped pharmacodynamic functions of single inhibitor effects of inhibitor 1 and inhibitor 2, Bliss independence and Loewe additivity models predict different effects of inhibitors in combination. The grey area marks all effects that are antagonistic according to Bliss independence and synergistic according to Loewe additivity.

Figure 2.

Diagrammatic representation of the multi-hit model. (a) Cells of the bacterial population N_tot are divided into classes according to how many inhibitors are attached to the cell surface. N_tot is the sum of all cells in all classes. The figure shows all classes for i ≤ 2, j ≤ 2; however, the matrix can be expanded. For reasons of simplicity, not all processes considered in the model are illustrated here and the attached inhibitors are not shown at the receptors of each cell. (b) Detailed depiction of all processes focusing on cell class N_1,1, in which one inhibitor molecule of each type is attached to the cells' surface. Note that the cell class N_1,1 is in the middle of the figure with one inhibitor molecule of each type attached to the receptors. 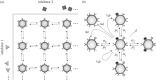Cells from this class transit to class N_2,1 at the rate and to class N_1,2 with the rate Cells from class N_0,1 transit to N_1,1 with the rate and from class N_1,0 with the rate . Inhibitors detach from the cells in class N_1,1 at the rates and respectively. The class N_1,1 gains cells through detachment of inhibitors from cells of higher classes with in the case of detachment of inhibitor 1 and in the case of detachment of inhibitor 2. The cells replicate at the rate b_1,1N_1,1; of all cells replicated, one-fourth stay in the class N_1,1 whereas each one-fourth of the cells are categorized to the classes N_0,1, N_1,0 and N_0,0, respectively. Lastly, cells can die at the rate d_1,1 N_1,1. Because we assumed the parameter to be the same independent of the class they are in, we use the following simplified expressions for the parameters: α₁ instead of α_1,1,1 and α_1,2,1, α₂ instead of α_2,1,1 and α_2,1,2, μ₁ instead of μ_1,1,1 and μ_1,2,1, μ₂ instead of μ_2,1,1 and μ_2,1,2, b instead of b_1,1, and d instead of d_1,1.

Figure 3.

Zombi class (grey box) of the multi-hit model. Here, τ₂ = 3 and therefore, N_1,2 enters the zombi class through attachment of one inhibitor 2 molecule (square-shaped molecules). In this class (N_1,3), inhibitors do not detach any more (μ_2,1,3 = 0), cells do not replicate any more (b_Z = b_1,3 = 0), and the cells are doomed to die with an increased death rate (d_Z = d_1,3 > d_1,2).

Figure 4.

Model assumptions and predictions of the independent and dependent-hit model. Receptors of the multi-hit models are different (a) and the same (d) for the two inhibitors in the independent-hit and dependent-hit model, respectively. (b) In the independent-hit model, the number of hits of inhibitor 1 needed to put a cell into the zombi class τ₁ is independent of τ₂ and vice versa. (e) The number of hits needed to put bacteria in the zombi class Z is dependent on both inhibitor types in the dependent-hit model. The model output and the estimated pharmacodynamic curve in the case of single drug application is illustrated in (c) for the independent-hit model (filled square inhibitor 1, filled triangle inhibitor 2) and in (f) for the dependent-hit model (open circle inhibitor 1 and 2). Note that single drug application in the dependent-hit model always gives the same output, regardless of the AMP type, whereas for the independent-hit model, the output is only the same if all parameters are the same (not shown here). All parameters used are listed in table 1.

Figure 5.

The number of hits necessary to kill a cell τ influences both EC₅₀ and κ positively. (a) The relationship between τ and EC₅₀ appears to be linear. (b) It is clearly a nonlinear relationship between τ and κ. Filled square inhibitor 1 (independent-hit model), filled triangle inhibitor 2 (independent-hit model), open circle inhibitor 1 and 2 (dependent-hit model). The results are the same for both inhibitor 1 and inhibitor 2 in the dependent-hit model due to the model assumptions. All parameters—except for τ, which we varied according to the x-axis of the figures—are listed in table 1. Note that τ₁ = τ₂ in the independent-hit framework.

Figure 6.

Contour plots of (a) the independent-hit model, (b) the Bliss independence reference model, (c) the dependent-hit model, and (d) the Loewe additivity reference model. The results of the multi-hit models (a,c) for single inhibitor application are used to fit pharmacodynamic curves. These curves are then used to determine the predicted additive effect for all combinations of the two types of inhibitors in the ad hoc reference models (b,d). The isobole of r(A₁, A₂) = 0 is marked as a bold line. All parameters used are listed in table 1.