Regulation of Irregular Neuronal Firing by Autaptic Transmission

Abstract

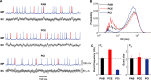
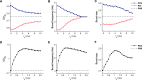
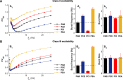
The importance of self-feedback autaptic transmission in modulating spike-time irregularity is still poorly understood. By using a biophysical model that incorporates autaptic coupling, we here show that self-innervation of neurons participates in the modulation of irregular neuronal firing, primarily by regulating the occurrence frequency of burst firing. In particular, we find that both excitatory and electrical autapses increase the occurrence of burst firing, thus reducing neuronal firing regularity. In contrast, inhibitory autapses suppress burst firing and therefore tend to improve the regularity of neuronal firing. Importantly, we show that these findings are independent of the firing properties of individual neurons, and as such can be observed for neurons operating in different modes. Our results provide an insightful mechanistic understanding of how different types of autapses shape irregular firing at the single-neuron level, and they highlight the functional importance of autaptic self-innervation in taming and modulating neurodynamics.

Figure 1. Schematic description of the computational model.

(A) Basic model architecture. In the model, the postsynaptic neuron receives balanced excitation-inhibition input from N_ex excitatory presynaptic neurons (EPN) and N_inh inhibitory presynaptic neurons (IPN). For simplicity, each presynaptic neuron is modelled as a Poisson spike train generator, with a fixed input rate f_in. In addition, the postsynaptic neuron is also driven by the self-feedback autaptic input from itself. (B) Five model versions used in our simulations. From (B₁)–(B₅), five models are termed as: the postsynaptic neuron with autapse blockade (PAB), the postsynaptic neuron with chemical excitatory autapse (PCE), the postsynaptic neuron with chemical inhibitory autapse (PCI), the comparative model (CM), and the postsynaptic neuron with electrical autapse (PEA), respectively. Note that the CM model is designed to compare with either the PCE or PCI model, in which the chemical autapse is replaced by an equivalent Poisson spike train (EPST) with both the same coupling type and firing rate.

Figure 2. Presynaptic bombardment contributes to the modulation of neuronal firing irregularity.

(A) The CV_ISI value is plotted as a function of the input rate f_in for the PAB model. The postsynaptic neuron achieves the best firing regularity at f_in = 6.3 Hz. (B) Typical membrane potential (MP) traces and corresponding synaptic current (SC) traces at different input rates. Here the red color in MP traces denotes the occurrence of burst firing. The black lines in SC traces represent the total synaptic currents from presynaptic neurons, and the gray lines in SC traces are zero-current levels. Four input rates considered in (B) are: f_in = 1.5 Hz, f_in = 6 Hz, f_in = 12 Hz and f_in = 30 Hz. (C) ISI distribution curves correspond to the above four input rates. Each ISI distribution curve is computed using 10⁵ firing events. (D) Dependence of the CV_ISI value on three key presynaptic-related parameters, which are the excitatory synaptic strength (D₁), the population size of presynaptic neurons (D₂) and the proportion of excitatory neurons (D₃). Two input rates considered in (D) are: f_in = 3 Hz and f_in = 6 Hz.

Figure 3. Roles of chemical autapses in modulating irregular neuronal firing.

(A–C) Dependence of the CV_ISI value (A), average output firing rate (B) and autaptic contribution factor (C) on the input rate f_in for the PCE and PAB models. In (A–C), the excitatory autaptic coupling strengths are: W_aut = 0.05 mS/cm² (PCE), W_aut = 0.1 mS/cm² (PCE) and W_aut = 0 mS/cm² (PAB). (D–F) Dependence of the CV_ISI value (D), average output firing rate (E) and autaptic contribution factor (F) on the input rate f_in for the PCI and PAB models. In (D–F), the inhibitory autaptic coupling strengths are: W_aut = 0.3 mS/cm² (PCI), W_aut = 0.6 mS/cm² (PCI) and W_aut = 0 mS/cm² (PAB). Simulations indicate that both excitatory and inhibitory autapses modulate the firing irregularity of neurons in the intermediate and high input regimes.

Figure 4. Statistics of burst firing explains the mechanisms of chemical autapses in shaping irregular neuronal firing.

(A) Typical MP traces and corresponding SC traces for the PAB, PCE and PCI models. Here the red color in MP traces denotes the occurrence of burst firing. The gray lines in SC traces represent the total synaptic currents from presynaptic neurons, and the black lines in SC traces are the autaptic currents from the postsynaptic neuron. (B) ISI distribution curves for the PAB, PCE and PCI models. (C) Burst frequency (C₁) and burst size (C₂) for the PAB, PCE and PCI models. In simulations, we set f_in = 40 Hz, and choose W_aut = 0.1 mS/cm² for the PCE model and W_aut = 0.6 mS/cm² for the PCI model. Note that the black dashed lines in (C₁) and (C₂) represent the burst frequency and burst size of the PAB model, respectively.

Figure 5. Chemical autaptic modulation on irregular neuronal firing cannot be accomplished by an equivalent “feedforward” synapse with stochastic inputs.

(A) Dpendence of the CV_ISI value (A₁) and average output firing rate (A₂) on the input rate f_in for the PCE, CM and PAB models. (B) Burst frequency (B₁) and burst size (B₂) for the PCE, CM and PAB models, which are driven by f_in = 40 Hz presynaptic trains. In (A,B), we set W_aut = 0.1 mS/cm² for the PCE model and the same coupling strength for the equivalent excitatory “feedforward” synapse in the CM model. (C) Dependence of the CV_ISI value (C₁) and average output firing rate (C₂) on the input rate f_in for the PCI, CM and PAB models. (D) Burst frequency (D₁) and burst size (D₂) for the PCI, CM and PAB models, which are driven by f_in = 40 Hz presynaptic trains. In (C,D), we set W_aut = 0.6 mS/cm² for the PCI model and the same coupling strength for the equivalent inhibitory “feedforward” synapse in the CM model. It should be noted that the black dashed lines in (B₁,D₁) and (B₂,D₂) represent the burst frequency and burst size of the PAB model, respectively.

Figure 6. Effect of electrical autapse in modulating irregular neuronal firing.

(A) The CV_ISI value (A₁) and average output firing rate (A₂) are plotted as a function of the input rate f_in for the PEA and PAB models. (B) Typical MP traces and corresponding SC traces of the PEA model at different self-feedback levels. Similar to Fig. 4A, the red color in MP traces denotes the occurrence of burst firing, the gray lines in SC traces represent the total synaptic currents from presynaptic neurons, and the black lines in SC traces are the autaptic currents from the postsynaptic neuron. (C) ISI distribution curves for the PEA and PAB models, with the input rate f_in = 40 Hz. (D) Burst frequency (D₁) and burst size (D₂) for the PEA and PAB models. In simulations, electrical coupling strengths are: W_aut = 0 mS/cm² (PAB), W_aut = 0.2 mS/cm² (PEA), W_aut = 0.4 mS/cm² (PEA) and W_aut = 0.6 mS/cm² (PEA). The black dashed lines in (D₁) and (D₂) represent the burst frequency and burst size of the PAB model, respectively.

Figure 7. Autaptic transmission delay participates into the modulation of irregular neuronal firing.

(A–C) Dependence of the CV_ISI value (A), burst frequency (B) and burst size (C) on the autaptic transmission delay τ_d for the PCE and PCI models. In each model, the postsynaptic neuron is driven by f_in = 40 Hz presynaptic trains. In simulations, we set W_aut = 0.1 mS/cm² for the PCE model and W_aut = 0.6 mS/cm² for the PCI model. The dashed lines in (A–C) represent the default CV_ISI value, burst frequency and burst size of the PAB model, respectively. (D–F) Dependence of the CV_ISI value (D), burst frequency (E) and burst size (F) on the autaptic transmission delay τ_d for the PEA model, which is driven by f_in = 40 Hz presynaptic trains. In simulations, we choose W_aut = 0.6 mS/cm² for the PEA model. As a comparison, the default CV_ISI value, burst frequency and burst size of the PAB model are also depicted in (D–F), respectively.

Figure 8. The main results based on class I neuron are extendable to spiking neurons with class II and III excitabilities.

(A,B) Simulations of the postsynaptic neuron with class II excitability (A) and with class III excitability (B). In (A₁,B₁), the CV_ISI value is plotted as a function of the input rate f_in under different autaptic coupling conditions. In (A₂,A₃), we show the burst frequency and burst size of the class II postsynaptic neuron driven by f_in = 8 Hz presynaptic trains. Similarly, the burst frequency and burst size of the class III postsynaptic neuron driven by f_in = 16 Hz presynaptic trains are illustrated in (B₂,B₃). For the class II postsynaptic neuron, we set W_aut = 0.05 mS/cm² for the PCE model, W_aut = 0.3 mS/cm² for the PCI model and W_aut = 0.3 mS/cm² for the PEA model. For the class III postsynaptic neuron, we set W_aut = 0.05 mS/cm² for the PCE model, W_aut = 0.3 mS/cm² for the PCI model and W_aut = 0.5 mS/cm² for the PEA model.