The Phase Lag between Agonist-Induced Oscillatory Ca2+ and IP3 Signals Does Not Imply Causality (December 2015)

Abstract

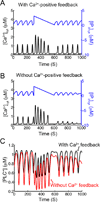
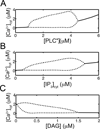
Activated phospholipase C (PLC*) generates 1,4,5-triphosphate (IP₃) and diacylglycerol (DAG) from phosphatidyl inositol (PIP₂). The DAG remains in the plasma membrane and co-activates conventional protein kinase C (PKC) with Ca²⁺. We have developed a mathematical model for the activation of the Ca²⁺-dependent PKC and its negative feedback on phospholipase C (PLC) and coupled it to the De Young-Keizer model for IP₃ mediated Ca²⁺ oscillations. The model describes the cascade of reactions for the translocation of PKC to plasma membrane, and simulates activation of Ca²⁺ and diacylglycerol (DAG) oscillations. The model demonstrates that oscillations in Ca²⁺ and DAG are possible with or without a positive Ca²⁺ feedback on phospholipase C consistent with experiment. In many experimental studies, the timing of the peaks of the Ca²⁺ and IP₃ oscillations have been used to suggest causality, i.e. that the IP₃ oscillations cause the Ca²⁺ oscillations. The model is used to explore this question. To this end, the positive and negative feedback between Ca²⁺ and IP₃ production are modulated, resulting in changes to the phase lag between the peaks in [Ca²⁺]_cyt and [IP]_cyt. The model simulates a possible experimental protocol that can be used to differentiate whether or not the positive feedback of Ca²⁺ on PLC is needed for the oscillations.

Keywords: calcium oscillation; computational model; diacyl glycerol (DAG); phospholipase C (PLC); protein kinase C (PKC).

Fig. 1

Model schematic. A. PLC activation pathway. (DAG – diacyl glycerol; PKC* - activated protein kinase C; PLC* – activated phospholipase C; IP₃ – inositol 1,4,5-trisphosphate; Ca²⁺ - calcium ion, v₁–v₆ – reaction rates). The dashed line indicates the positive feedback of Ca²⁺ on PLC which is explored further in this study. B. Reaction scheme for PKC activation. (PKC_c – cytoplasmic PKC; PKC_m – membrane associated PKC; k₁–k₈ reaction rates).

Fig. 2

Simulated time courses of concentrations. A. Simulated intracellular Ca²⁺, DAG binding domains of PKC-C1 (PKC_m:DAG) oscillations when PLC is active (top panel). The translocation of C1 is delayed by a few seconds. B. Activated PKC (PKC^*) oscillations are almost in-phase with Ca²⁺ transit. C. Activated PLC ([PLC*]), DAG and IP₃ show in-phase oscillations.

Fig. 3

Simulated time courses of concentrations. A. Free PKC concentrations in the cytosol [PKC_c] and PKC concentrations associated with the plasma membrane [PKC_m] oscillate during PLC activation pathway. B. PKC bound to Ca²⁺ in cytoplasm ([PKC_c:Ca²⁺]), and C. Ca²⁺ binding of PKC-C2 domains translocate to plasma membrane ([PKC_m:Ca²⁺]) both oscillate during Ca²⁺ oscillations.

Fig. 4

Phase maps. A. The effects of positive feedback of Ca²⁺ and negative feedback of PKC* on Ca²⁺ and DAG oscillations. These plots show the phase difference between the [Ca²⁺]_cyt and [IP₃]_cyt oscillation peaks. The phase difference is calculate as 360*((time of Ca²⁺ peak) - (time of DAG peak))/(oscillation period), In this way when the periods are aligned the value is 0, when they are opposite in phase it is 180. The synchronization between Ca²⁺ and DAG oscillations varies with feedback strength. B. The changing of the degradation rate of IP₃ (v₅) affects the phase differences of Ca²⁺ and IP₃. When v₆ (Ca²⁺ dependent rate of PLC activation) large, the oscillations of calcium and IP₃ are in phase. The default model parameter is shown by the red circle. C. The Ca²⁺ dependent rate of PLC activation (v₆) and Ca²⁺ dependent rate k_plcon for positive feedback affect the phase differences of Ca²⁺ and IP₃. The default model parameter is shown by the red circle.

Fig. 5

Ca²⁺ oscillations affect IP₃ and activated PLC ([PLC*]) oscillations. A. There is no IP₃ oscillation when Ca²⁺ is set to a constant level (1.0 µM). B. Blocking DAG degradation eliminates [PLC*] oscillation (dashed line), whereas DAG degradation results in PLC oscillations (solid line).

Fig. 6

Blocking the feedbacks on PLC affect Ca²⁺ dynamics. A. There are no Ca²⁺ oscillations and the IP₃ rise by blocking PKC. Furthermore, the IP₃ concentration rises as there is no negative feedback on PLC. B. When the positive feedback of Ca²⁺ on PLC is eliminated the IP₃ concentration returns to steady state. C. When the positive feedback of Ca²⁺ on PLC is eliminated the Ca²⁺ concentration also returns to steady-state level. However, if the mean [IP₃]_cyt is raised, [Ca²⁺]_cyt oscillations can occur in the absence of positive feedback of Ca²⁺ on PLC (see Figure 8).

Fig. 7

Test to see if positive feedback of Ca²⁺ on PLC is involved with [Ca²⁺]_cyt oscillations. An applied IP₃ pulse as shown results in different behaviors in the models with and without positive feedback of Ca²⁺ on PLC. In both cases the [Ca²⁺]_cyt oscillation frequency increases with the increased [IP₃]_cyt. A. In the model with positive feedback of Ca²⁺ on PLC, the oscillations resume similar to those before the pulse. B. In the model without positive feedback of Ca²⁺ on PLC, the [Ca²⁺]_cyt oscillations do not resume. C. The time course for activated [PLC] shows differing dynamics in the system with Ca²⁺ feedback on PLC (black) and without Ca²⁺ feedback on PLC (red).

Fig. 8

Bifurcation diagrams for Ca²⁺ oscillations (——) indicates stable steady states and (-------) gives maximum and minimum [Ca²⁺]_cyt during oscillations. A. The model generates oscillations in Ca²⁺ while [PLC*] between 1 and 4.2 µM. B. The constant IP₃ ([IP₃] + [IP₃β]) between 0.8 and 4.4 µM can produce Ca²⁺ oscillations. C. [DAG] can affect Ca²⁺ oscillations when set [DAG] to a constant in between 0.0 and 2.0 µM.