Intermediate-Range Migration Furnishes a Narrow Margin of Efficiency in the Two-Strategy Competition

Abstract

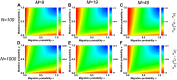
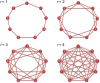
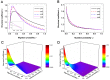
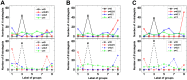
It is well-known that the effects of spatial selection on the two-strategy competition can be quantified by the structural coefficient σ under weak selection. We here calculate the accurate value of σ in group-structured populations of any finite size. In previous similar models, the large population size has been explicitly required for obtaining σ, and here we analyze quantitatively how large the population should be. Unlike previous models which have only involved the influences of the longest and the shortest migration rang on σ, we consider all migration ranges together. The new phenomena are that an intermediate range maximizes σ for medium migration probabilities which are of the tiny minority and the maximum value is slightly larger than those for other ranges. Furthermore, we find the ways that migration or mutation changes σ can vary significantly through determining analytically how the high-frequency steady states (distributions of either strategy over all groups) impact the expression of σ obtained before. Our findings can be directly used to resolve the dilemma of cooperation and provide a more intuitive understanding of spatial selection.

Fig 1. The comparison of the accurate structural coefficientσ_ac, the approximate one σ_ap, and the one from the Monte Carlo simulation across various mutation probabilities (u) and various migration probabilities (v).

(A)-(D) shows that σ_ac (solid line) is in agreement with the one from Monte Carlo simulations (square, averaged over 10⁹ generations) for all v and all u, and σ_ap (dashed line) is in line with the one from the Monte Carlo simulation (square, averaged over 10⁹ generations) for low v and has a significance difference from the one from the Monte Carlo simulation (square, averaged over 10⁹ generations) for high v. Parameters: N = 100, M = 19.

Fig 2. Comparison of the accurate structural coefficientσ_ac and the approximate one σ_ap across the parameter space (v, u).

A population of size N = 100 (A, B, C) or N = 1000 (D, E, F) is distributed over M = 9 (A, D), M = 19 (B, E), M = 49 (C, F) groups, respectively. The relative difference of σ_ac and σ_ap, |σ_ac−σ_ap|/σ_ac, decreases as N rises (each column) or as M diminishes (each row), and it is small when u or v is low (each panel). Note the same color in all panels represents different values.

Fig 3. Migration patterns characterized by the migration ranger.

Nine groups (red node) are arranged in a regular circle and labelled from 1 to 9 in clockwise. An edge exists between two nodes if and only if there is a potential single-step migration path between them. In other words, an offspring can migrate to one of the nodes connected to the node in which the parent is located. The distance between two groups takes on one of the values 1, 2, 3, 4. The migration range r means that the set of the displacements that a single-step migration leads to is Ω(r) = {1,⋯,r}.

Fig 4. The structural coefficient σ depends on the migration probability v, the mutation probability u, and the migration range r.

Panel (A) shows that for each r, σ first increases and then decreases when v grows, and among all migration ranges the one leading to the largest value of σ is r = 4 for low v, r = 2,3 for medium v (see the inset), and r = 1 for high v. Panel (B) demonstrates that for each r, σ diminishes as u increases. We also give a whole view of how σ changes with u and v for r = 1 (panel (C)) and for r = 4 (panel (D)) which can verify the universality of the phenomena in panel (C) and panel (D). Parameters: N = 100, M = 9, (A) u = 0.07, (B) v = 0.1.

Fig 5. The distribution of strategy A and the one of strategy B over all groups.

The above panels exhibit the distributions of strategy A over M = 9 groups and the below the distributions of strategy B over M = 9 groups at generation 10⁸ (A), generation 5 × 10⁸ (B), and generation 9 × 10⁸ (C). For the migration probability v = 0 (◻), all individuals are centered in one group; for v = 0.01 (◯) and for v = 0.1 (△), more groups are taken up and individuals of a given strategy are distributed unevenly over groups; for v = 1 (⋄), all groups are occupied and the distribution of each strategy over nine groups becomes more uniform. Parameters: N = 100, M = 9, u = 0.07, r = 1.