Mapped Chebyshev pseudo-spectral method for simulating the shear wave propagation in the plane of symmetry of a transversely isotropic viscoelastic medium

Abstract

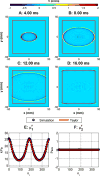
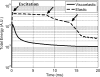
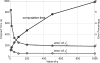
Shear wave elastography is a versatile technique that is being applied to many organs. However, in tissues that exhibit anisotropic material properties, special care must be taken to estimate shear wave propagation accurately and efficiently. A two-dimensional simulation method is implemented to simulate the shear wave propagation in the plane of symmetry in transversely isotropic viscoelastic media. The method uses a mapped Chebyshev pseudo-spectral method to calculate the spatial derivatives and an Adams-Bashforth-Moulton integrator with variable step sizes for time marching. The boundaries of the two-dimensional domain are surrounded by perfectly matched layers to approximate an infinite domain and minimize reflection errors. In an earlier work, we proposed a solution for estimating the apparent shear wave elasticity and viscosity of the spatial group velocity as a function of rotation angle through a low-frequency approximation by a Taylor expansion. With the solver implemented in MATLAB, the simulated results in this paper match well with the theory. Compared to the finite element method simulations we used before, the pseudo-spectral solver consumes less memory and is faster and achieves better accuracy.

Keywords: Perfectly matched layer; Pseudo-spectral method; Shear wave; Transversely isotropic; Viscoelastic.

Figure 1

Setup for the transversely isotropic medium to be simulated. Direction of the tissue fibers is along the x axis. Plane x-y is the plane of symmetry P_s. Excitation is applied in the center of the plane and the generated shear waves travel radially from the source to the outside boundaries.

Figure 2

2D mesh grid before (A) and after (B) mapping. The two plots around each figure are the grid spacing in x and y directions. The domains of both directions are [−1, +1] meters. The numbers of points in both directions are 32. The parameters of the polynomial mappings in both directions are a = 0.2 and p = 2.0. the mapping procedures increase the mesh size around the boundaries and decrease the mesh size around the center.

Figure 3

Shear wave propagation. ${\mu }_1^x=25\mathrm{kPa}$, ${\mu }_1^y=9\mathrm{kPa}$, ${\mu }_2^x=8\mathrm{Pa}\cdot \mathrm{s}$, ${\mu }_2^y=3\mathrm{Pa}\cdot \mathrm{s}$. A–D: the waveform at 4, 8, 12 and 16 ms, respectively. The area enclosed by the red square does not have PML damping. E and F: group elasticity ${\mu }_1^r$ and viscosity ${\mu }_2^r$ estimated from simulation and its comparison with Equations 22 and 23.

Figure 4

Shear wave propagation. ${\mu }_1^x=25\mathrm{kPa}$, ${\mu }_1^y=9\mathrm{kPa}$, ${\mu }_2^x=0\mathrm{Pa}\cdot \mathrm{s}$, ${\mu }_2^y=0\mathrm{Pa}\cdot \mathrm{s}$. A–D: the waveform at 4, 8, 12 and 16 ms, respectively. The area enclosed by the red square does not have PML damping. E and F: group elasticity ${\mu }_1^r$ and viscosity ${\mu }_2^r$ estimated from simulation and its comparison with Equations 22 and 23.

Figure 5

Total energy as a function of elapsed time. For the elastic wave simulation, the transition points near 8 ms and 13 ms (denoted by arrows) are caused by the PML for the wave in x and y directions, respectively. The rise at the beginning of the simulation is the occurrence of the excitation.

Figure 6

A: Normalized particle velocities at y = 8.5 mm simulated by the implemented pseudo-spectral method and a FEM method. The material is a transversely isotropic, elastic medium with ${\mu }_1^x=25\mathrm{kPa}$ and ${\mu }_1^y=9\mathrm{kPa}$. The mesh density in the plane of symmetry for the FEM method is 30% higher than that of the pseudo-spectral method. B: Percentage of change of the maximum particle velocity at y = 8.5 mm relative to the finest mesh density.

Figure 7

Comparison of the number of time steps to reach the same simulated time between mapped (solid line) and unmapped (dashed line) Chebyshev methods. The material properties are: ${\mu }_1^x=25\mathrm{kPa}$, ${\mu }_1^y=9\mathrm{kPa}$, ${\mu }_2^x=0\mathrm{Pa}\cdot \mathrm{s}$, ${\mu }_2^y=0\mathrm{Pa}\cdot \mathrm{s}$.

Figure 8

The impacts of value of q on the computation time and errors. The max percentage of error was calculated by $\mathit{max}\left(\frac{|\mathit{Estimated}\mathit{Value}-\mathit{Taylor}\mathit{Expansion}|}{\mathit{Taylo}r\mathit{Expansion}}\right)\times 100\%$, as shown in the subfigures E and F of Figure 3. Material properties ${\mu }_1^x=25\mathrm{kPa}$, ${\mu }_1^y=9\mathrm{kPa}$, ${\mu }_2^x=8\mathrm{Pa}\cdot \mathrm{s}$, ${\mu }_2^y=3\mathrm{Pa}\cdot \mathrm{s}$.