Chromosome Compaction by Active Loop Extrusion
- PMID: 27224481
- PMCID: PMC4880799
- DOI: 10.1016/j.bpj.2016.02.041
Chromosome Compaction by Active Loop Extrusion
Abstract
During cell division, chromosomes are compacted in length by more than a 100-fold. A wide range of experiments demonstrated that in their compacted state, mammalian chromosomes form arrays of closely stacked consecutive ∼100 kb loops. The mechanism underlying the active process of chromosome compaction into a stack of loops is unknown. Here we test the hypothesis that chromosomes are compacted by enzymatic machines that actively extrude chromatin loops. When such loop-extruding factors (LEF) bind to chromosomes, they progressively bridge sites that are further away along the chromosome, thus extruding a loop. We demonstrate that collective action of LEFs leads to formation of a dynamic array of consecutive loops. Simulations and an analytically solved model identify two distinct steady states: a sparse state, where loops are highly dynamic but provide little compaction; and a dense state, where there are more stable loops and dramatic chromosome compaction. We find that human chromosomes operate at the border of the dense steady state. Our analysis also shows how the macroscopic characteristics of the loop array are determined by the microscopic properties of LEFs and their abundance. When the number of LEFs are used that match experimentally based estimates, the model can quantitatively reproduce the average loop length, the degree of compaction, and the general loop-array morphology of compact human chromosomes. Our study demonstrates that efficient chromosome compaction can be achieved solely by an active loop-extrusion process.
Copyright © 2016 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures
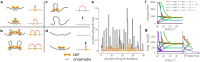
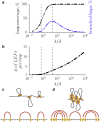


Comment in
-
Extruding Loops to Make Loopy Globules?Biophys J. 2016 May 24;110(10):2133-5. doi: 10.1016/j.bpj.2016.04.008. Biophys J. 2016. PMID: 27224477 Free PMC article. No abstract available.
References
-
- Maeshima K., Laemmli U.K. A two-step scaffolding model for mitotic chromosome assembly. Dev. Cell. 2003;4:467–480. - PubMed
-
- Maeshima K., Eltsov M., Laemmli U.K. Chromosome structure: improved immunolabeling for electron microscopy. Chromosoma. 2005;114:365–375. - PubMed
-
- Paulson J.R., Laemmli U.K. The structure of histone-depleted metaphase chromosomes. Cell. 1977;12:817–828. - PubMed
-
- Marsden M.P., Laemmli U.K. Metaphase chromosome structure: evidence for a radial loop model. Cell. 1979;17:849–858. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

