Crystal Nucleation in Liquids: Open Questions and Future Challenges in Molecular Dynamics Simulations
- PMID: 27228560
- PMCID: PMC4919765
- DOI: 10.1021/acs.chemrev.5b00744
Crystal Nucleation in Liquids: Open Questions and Future Challenges in Molecular Dynamics Simulations
Abstract
The nucleation of crystals in liquids is one of nature's most ubiquitous phenomena, playing an important role in areas such as climate change and the production of drugs. As the early stages of nucleation involve exceedingly small time and length scales, atomistic computer simulations can provide unique insights into the microscopic aspects of crystallization. In this review, we take stock of the numerous molecular dynamics simulations that, in the past few decades, have unraveled crucial aspects of crystal nucleation in liquids. We put into context the theoretical framework of classical nucleation theory and the state-of-the-art computational methods by reviewing simulations of such processes as ice nucleation and the crystallization of molecules in solutions. We shall see that molecular dynamics simulations have provided key insights into diverse nucleation scenarios, ranging from colloidal particles to natural gas hydrates, and that, as a result, the general applicability of classical nucleation theory has been repeatedly called into question. We have attempted to identify the most pressing open questions in the field. We believe that, by improving (i) existing interatomic potentials and (ii) currently available enhanced sampling methods, the community can move toward accurate investigations of realistic systems of practical interest, thus bringing simulations a step closer to experiments.
Conflict of interest statement
The authors declare no competing financial interest.
Figures

 , as a function of the crystalline nucleus
size n. A free energy barrier for nucleation,
, as a function of the crystalline nucleus
size n. A free energy barrier for nucleation,  , must
be overcome to proceed from the (metastable)
supercooled liquid state to the thermodynamically stable crystalline
phase through homogeneous nucleation (purple). Heterogeneous nucleation
(green) can be characterized by a lower free energy barrier,
, must
be overcome to proceed from the (metastable)
supercooled liquid state to the thermodynamically stable crystalline
phase through homogeneous nucleation (purple). Heterogeneous nucleation
(green) can be characterized by a lower free energy barrier,  , and a smaller critical nucleus size, nhet*, whereas
in the case of spinodal decomposition (orange), the supercooled
liquid is unstable with respect to the crystalline phase, and the
transformation to the crystal proceeds in a barrierless fashion. The
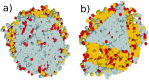
three snapshots depict a crystalline cluster nucleating within the
supercooled liquid phase (homogeneous nucleation) or as a result of
the presence of a foreign impurity (heterogeneous nucleation), as
well as the simultaneous occurrence of multiple crystalline clusters
in the unstable liquid. This scenario is often labeled as spinodal
decomposition, although the existence of a genuine spinodal decomposition
from the supercooled liquid to the crystalline phase has been debated
(see text).
, and a smaller critical nucleus size, nhet*, whereas
in the case of spinodal decomposition (orange), the supercooled
liquid is unstable with respect to the crystalline phase, and the
transformation to the crystal proceeds in a barrierless fashion. The
three snapshots depict a crystalline cluster nucleating within the
supercooled liquid phase (homogeneous nucleation) or as a result of
the presence of a foreign impurity (heterogeneous nucleation), as
well as the simultaneous occurrence of multiple crystalline clusters
in the unstable liquid. This scenario is often labeled as spinodal
decomposition, although the existence of a genuine spinodal decomposition
from the supercooled liquid to the crystalline phase has been debated
(see text).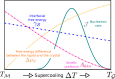
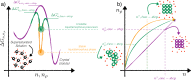
 , the interfacial free energy
, the interfacial free energy  , and the kinetic prefactor
, and the kinetic prefactor  are reported as functions of ΔT in a generic case of diffusion-limited nucleation, characterized
by a maximum in the steady-state nucleation rate
are reported as functions of ΔT in a generic case of diffusion-limited nucleation, characterized
by a maximum in the steady-state nucleation rate  .
.  is zero at the melting temperature
is zero at the melting temperature  , and
, and  is vanishingly
small at the glass transition
temperature
is vanishingly
small at the glass transition
temperature  .
.

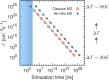
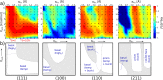
 as a
function of the simulation time needed
within an MD simulation to observe a single nucleation event. The
blue shaded region highlights the approximate simulation times currently
affordable by classical MD simulations; clearly, only very fast nucleation
processes can be simulated with brute-force MD. For homogeneous ice
nucleation,
as a
function of the simulation time needed
within an MD simulation to observe a single nucleation event. The
blue shaded region highlights the approximate simulation times currently
affordable by classical MD simulations; clearly, only very fast nucleation
processes can be simulated with brute-force MD. For homogeneous ice
nucleation,  and
and  can typically be observed for ΔT = 30 K and
ΔT = 80 K, respectively.
In the derivations of classical and ab initio simulation times, 105 and 102 molecules, respectively, were considered,
together with the number density of a generic supercooled liquid,
can typically be observed for ΔT = 30 K and
ΔT = 80 K, respectively.
In the derivations of classical and ab initio simulation times, 105 and 102 molecules, respectively, were considered,
together with the number density of a generic supercooled liquid,  = 0.01 molecules·Å–3.
= 0.01 molecules·Å–3.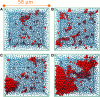
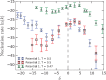






 , are
reported as log10(J/J0), where J0 refers to the
homogeneous nucleation rate at the same
temperature. (b) Sketches of the different regions (white areas) in
(Eads,afcc) space in which a significant enhancement of the nucleation rate
is observed. Each region is labeled according to the face of Ih nucleating and growing on top of the surface [basal, prismatic,
or (11/
, are
reported as log10(J/J0), where J0 refers to the
homogeneous nucleation rate at the same
temperature. (b) Sketches of the different regions (white areas) in
(Eads,afcc) space in which a significant enhancement of the nucleation rate
is observed. Each region is labeled according to the face of Ih nucleating and growing on top of the surface [basal, prismatic,
or (11/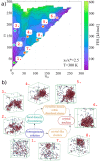

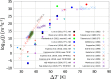
 , as a function
of the driving force for
nucleation, reported as 1/(Δμ/kBT)2. Red points and blue and gray (continuous)
lines were estimated by three different approaches in the simulations
of Zimmermann et al. Experimental data
obtained employing an electrodynamic levitator trap (Na et al.), an efflorescence chamber (Gao et al.), and microcapillaries (Desarnaud et al.) are also reported, together with a tentative
fit (γfitexp, dotted line). Note the substantial (up to about 30 orders of magnitude)
discrepancy between experiments and simulations. Reprinted with permission
from ref (402). Copyright
2015 American Chemical Society.
, as a function
of the driving force for
nucleation, reported as 1/(Δμ/kBT)2. Red points and blue and gray (continuous)
lines were estimated by three different approaches in the simulations
of Zimmermann et al. Experimental data
obtained employing an electrodynamic levitator trap (Na et al.), an efflorescence chamber (Gao et al.), and microcapillaries (Desarnaud et al.) are also reported, together with a tentative
fit (γfitexp, dotted line). Note the substantial (up to about 30 orders of magnitude)
discrepancy between experiments and simulations. Reprinted with permission
from ref (402). Copyright
2015 American Chemical Society.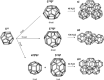
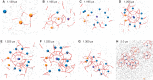
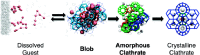
References
-
- Murray B. J.; Wilson T. W.; Dobbie S.; Cui Z.; Al-Jumur S. M. R. K.; Möhler O.; Schnaiter M.; Wagner R.; Benz S.; Niemand M.; et al. Heterogeneous Nucleation of Ice Particles on Glassy Aerosols under Cirrus Conditions. Nat. Geosci. 2010, 3, 233–237. 10.1038/ngeo817. - DOI
-
- Erdemir D.; Lee A. Y.; Myerson A. S. Polymorph Selection: The Role of Nucleation, Crystal Growth and Molecular Modeling. Curr. Opin. Drug. Discovery Dev. 2007, 10, 746–755. - PubMed
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
Miscellaneous

