Modelling the penumbra in Computed Tomography1
- PMID: 27232198
- PMCID: PMC4969716
- DOI: 10.3233/XST-160576
Modelling the penumbra in Computed Tomography1
Abstract
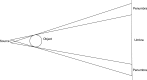
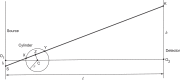
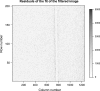
Background: In computed tomography (CT), the spot geometry is one of the main sources of error in CT images. Since X-rays do not arise from a point source, artefacts are produced. In particular there is a penumbra effect, leading to poorly defined edges within a reconstructed volume. Penumbra models can be simulated given a fixed spot geometry and the known experimental setup.
Objective: This paper proposes to use a penumbra model, derived from Beer's law, both to confirm spot geometry from penumbra data, and to quantify blurring in the image.
Methods: Two models for the spot geometry are considered; one consists of a single Gaussian spot, the other is a mixture model consisting of a Gaussian spot together with a larger uniform spot.
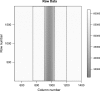
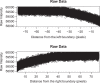
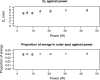
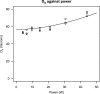
Results: The model consisting of a single Gaussian spot has a poor fit at the boundary. The mixture model (which adds a larger uniform spot) exhibits a much improved fit. The parameters corresponding to the uniform spot are similar across all powers, and further experiments suggest that the uniform spot produces only soft X-rays of relatively low-energy.
Conclusions: Thus, the precision of radiographs can be estimated from the penumbra effect in the image. The use of a thin copper filter reduces the size of the effective penumbra.
Keywords: Computed tomography; focal spot; nonlinear least squares; penumbra; secondary radiation.
Figures




Similar articles
-
Accurate technique for complete geometric calibration of cone-beam computed tomography systems.Med Phys. 2005 Apr;32(4):968-83. doi: 10.1118/1.1869652. Med Phys. 2005. PMID: 15895580
-
Effects of ray profile modeling on resolution recovery in clinical CT.Med Phys. 2014 Feb;41(2):021907. doi: 10.1118/1.4862510. Med Phys. 2014. PMID: 24506628
-
Imaging properties of digital magnification radiography.Med Phys. 2006 Apr;33(4):984-96. doi: 10.1118/1.2174133. Med Phys. 2006. PMID: 16696475
-
Lateral dose profile characterization in scanning particle therapy.Med Phys. 2011 Jun;38(6):2904-13. doi: 10.1118/1.3578603. Med Phys. 2011. PMID: 21815365
-
Effects of focal spot intensity distribution and collimator width in reconstructive x-ray tomography.Med Phys. 1979 May-Jun;6(3):229-32. doi: 10.1118/1.594570. Med Phys. 1979. PMID: 470849
Cited by
-
Markov random field segmentation for industrial computed tomography with metal artefacts.J Xray Sci Technol. 2018;26(4):573-591. doi: 10.3233/XST-17322. J Xray Sci Technol. 2018. PMID: 29562573 Free PMC article.
-
Improving resolution of head and neck CTA using the small x-ray tube focal spot.Neuroradiology. 2019 Aug;61(8):953-956. doi: 10.1007/s00234-019-02221-0. Epub 2019 May 18. Neuroradiology. 2019. PMID: 31104077
References
-
- Bates D.M. and Watts. D.G.. Nonlinear Regression Analysis and Its Applications John Wiley & Sons: 1988.
-
- Birch R., The spectrum and intensity of extra-focal (off-focus) radiation. British Journal of Radiology 49 (1976), 951–955. - PubMed
-
- British Standards Institution, BS EN 16016 (2011).
-
- Boone M.N., Vlassenbroeck J., Peetermans S., Van Loo D.. Dierick M and Van Hoorebeke L, Secondary radiation in transmission-type x-ray tubes: Simulation, practical issues and solution in the context of x-ray microtomography. Nuclear Instrumentation Methods Physics Research Section A 661 (2012), 7–12.
-
- Carmignato S., Accuracy of industrial computed tomography measurements: Experimental results from an international comparison. CIRP Annals - Manufacturing Technology 61 (2012), 491–494.
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

