Quantum-limited heat conduction over macroscopic distances

Abstract

The emerging quantum technological apparatuses1, 2, such as the quantum computer3-6, call for extreme performance in thermal engineering7. Cold distant heat sinks are needed for the quantized electric degrees of freedom due to the increasing packaging density and heat dissipation. Importantly, quantum mechanics sets a fundamental upper limit for the flow of information and heat, which is quantified by the quantum of thermal conductance8-10. However, the short distance between the heat-exchanging bodies in the previous experiments11-14 hinders their applicability in quantum technology. Here, we present experimental observations of quantum-limited heat conduction over macroscopic distances extending to a metre. We achieved this improvement of four orders of magnitude in the distance by utilizing microwave photons travelling in superconducting transmission lines. Thus, it seems that quantum-limited heat conduction has no fundamental distance cutoff. This work establishes the integration of normal-metal components into the framework of circuit quantum electrodynamics15-17 which provides a basis for the superconducting quantum computer18-21. Especially, our results facilitate remote cooling of nanoelectronic devices using far-away in-situ-tunable heat sinks22, 23. Furthermore, quantum-limited heat conduction is important in contemporary thermodynamics24, 25. Here, the long distance may lead to ultimately efficient mesoscopic heat engines with promising practical applications26.

Figure 1. Sample structure and measurement scheme.

a, Schematic illustration of a coplanar transmission line terminated at different ends by resistances R_A and R_B at electron temperatures T_A and T_B, respectively. b, Scanning electron microscope (SEM) image of a fabricated transmission line with a double-spiral structure. c, h, False-colour SEM images of the normal-metal islands together with a simplified measurement scheme. e, Optical micrograph of the waveguide. f, Atomic force microscope image of Island B highlighting the thicknesses of the nanostructures. g, SEM image showing how the normal-metal island is connected to the ground plane and to the centre conductor. Micrographs (c, f, g, h) are from Sample A1, and (b, e) are from a similar sample. h, Thermal model indicating the thermal conductance between the Islands A and B, G_AB, and those from the islands to the phonon bath at the temperature T₀, G_A0 and G_B0. Constant powers P_const,A/B and control power P_NIS are also indicated by arrows. i, Schematic diagram for cooling of the normal metal due to single-electron tunnelling (arrows) in a pair of NIS junctions biased at voltage $V_{\text{B}}\lesssim 2\Delta /e$. The densities of states in the superconductors (S) are shown by black solid lines whereas the Fermi distribution is indicated in the normal metal (N).

Figure 2. Photonic cooling at macroscopic distances for Sample A1.

a, b, Measured (a) and theoretically predicted (b) electron temperature changes with respect to the zero-bias case (V_B = 0) for Island A as functions of the voltage V_B and bath temperature T₀. At each T₀, the maximum cooling is obtained at V_B ≈ 0.4 mV ≈ 2Δ/e, as indicated by the white arrows. c, d, As in panels (a, b), but for temperature changes of Island B. e, Measured (markers) and simulated (lines) temperature changes at the maximum cooling point as functions of the bath temperature. The errorbars indicate the standard deviation of the measured temperatures. f, The ratio of the temperature changes in (e). 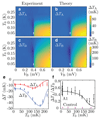Measurement results from the control sample () are shown for comparison.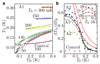

Figure 3. Differential temperature response and the quantum of thermal conductance.

a, Measured (dots) and simulated (dashed lines) temperatures of Island A as functions of the temperature of Island B for the indicated phonon bath temperatures in Sample A1. The results for the control sample at 100-mK bath temperature are shown for comparison. b, Differential temperature response () from (a) at the lowest T_B for each bath temperature. The experimental uncertainty is of the order of the marker size. For comparison, we also show the corresponding experimental data for the control sample (), for Sample A2 (), and for A3 (). The solid black line shows the prediction of the full thermal model of Supplementary Fig. 2. The dashed lines are calculated with 80 % (bottom) and 115 % (top) of the quantum of thermal conductance indicating the sensitivity of the results to the photonic heat conduction. The solid red lines are calculated with the simplified thermal model (equation (2)) for Sample A1 with electron–phonon coupling constants Σ_N↓ = 2 × 10⁹ WK⁻⁵m⁻³ (right), and Σ_N↑ = 4 × 10⁹ WK⁻⁵m⁻³ (left). The inset shows the extracted fraction η = G_AB/G_Q for Sample A1 for the simplified model with Σ_N↓ () and Σ_N↑ () and for the full thermal model () as functions of T₀.