Customized Steady-State Constraints for Parameter Estimation in Non-Linear Ordinary Differential Equation Models

Abstract

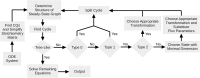
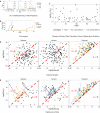
Ordinary differential equation models have become a wide-spread approach to analyze dynamical systems and understand underlying mechanisms. Model parameters are often unknown and have to be estimated from experimental data, e.g., by maximum-likelihood estimation. In particular, models of biological systems contain a large number of parameters. To reduce the dimensionality of the parameter space, steady-state information is incorporated in the parameter estimation process. For non-linear models, analytical steady-state calculation typically leads to higher-order polynomial equations for which no closed-form solutions can be obtained. This can be circumvented by solving the steady-state equations for kinetic parameters, which results in a linear equation system with comparatively simple solutions. At the same time multiplicity of steady-state solutions is avoided, which otherwise is problematic for optimization. When solved for kinetic parameters, however, steady-state constraints tend to become negative for particular model specifications, thus, generating new types of optimization problems. Here, we present an algorithm based on graph theory that derives non-negative, analytical steady-state expressions by stepwise removal of cyclic dependencies between dynamical variables. The algorithm avoids multiple steady-state solutions by construction. We show that our method is applicable to most common classes of biochemical reaction networks containing inhibition terms, mass-action and Hill-type kinetic equations. Comparing the performance of parameter estimation for different analytical and numerical methods of incorporating steady-state information, we show that our approach is especially well-tailored to guarantee a high success rate of optimization.

Keywords: biochemical reaction networks; multi-stability; multiplicity; non-linear ODE models; parameter estimation; positive solutions; steady-state; success rate.

Figure 1

Flowchart of Steady-State Determination: After identification of all CQs of the system, the algorithm performs a loop where in each pass one cycle of the steady-state graph is removed. Since for each cycle the nodes are analyzed with regard to the number of in- and outflux rates, the graph structure as well as the structure of the steady-state equations is kept as simple as possible. Once the steady-state graph is tree-like, the remaining equations are solved and equations are returned.

Figure 2

Optimization results for different steady-state parameterizations. Data was simulated for three different displacements of A at t = 30 (A). Convergent fits for all four steady-state implementations were sorted by increasing objective value (B). Steps correspond to local minima. Positive steady-state parameterizations show a considerably better convergence behavior. Starting samples are shown in different colors in (C,D), indicating whether the corresponding optimization converged. Parameter paths starting with k₀ < k₁ did mostly not converge as opposed to samples with k₀ > k₁ which mostly converged to a local or the global optimum G (E,F).

Figure 3

Optimization in the context of multiple steady-states. Data was simulated for three different displacements of A at t = 30 (A). Convergent fits from 200 starting samples for three different steady-state implementations were sorted by their final objective value (B). Fits that did not converge are not shown. In about 10% of the fits, the Standard and the Numeric approach converged, in the Proposed approach nearly 50% did. For each end point of the 200 numerical optimizations, the ratio A_num ∕ A₂ between the numerical solution A_num and the stable, analytical steady-state solution A₂ was computed (C). For A_num ∕ A₂ > 0, the numerical root calculation converged to the unstable steady-state which effects the abort of the optimization. Starting samples are shown in different colors, indicating whether the corresponding optimization converged. Many parameter samples starting with discriminant Δ < 0 did not converge, while most of the samples with Δ > 0 converged to the global optimum G, (D,E).