The Role of Adaptation in Bacterial Speed Races

Abstract

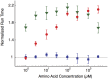
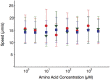
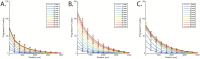
Evolution of biological sensory systems is driven by the need for efficient responses to environmental stimuli. A paradigm among prokaryotes is the chemotaxis system, which allows bacteria to navigate gradients of chemoattractants by biasing their run-and-tumble motion. A notable feature of chemotaxis is adaptation: after the application of a step stimulus, the bacterial running time relaxes to its pre-stimulus level. The response to the amino acid aspartate is precisely adapted whilst the response to serine is not, in spite of the same pathway processing the signals preferentially sensed by the two receptors Tar and Tsr, respectively. While the chemotaxis pathway in E. coli is well characterized, the role of adaptation, its functional significance and the ecological conditions where chemotaxis is selected, are largely unknown. Here, we investigate the role of adaptation in the climbing of gradients by E. coli. We first present theoretical arguments that highlight the mechanisms that control the efficiency of the chemotactic up-gradient motion. We discuss then the limitations of linear response theory, which motivate our subsequent experimental investigation of E. coli speed races in gradients of aspartate, serine and combinations thereof. By using microfluidic techniques, we engineer controlled gradients and demonstrate that bacterial fronts progress faster in equal-magnitude gradients of serine than aspartate. The effect is observed over an extended range of concentrations and is not due to differences in swimming velocities. We then show that adding a constant background of serine to gradients of aspartate breaks the adaptation to aspartate, which results in a sped-up progression of the fronts and directly illustrate the role of adaptation in chemotactic gradient-climbing.

Fig 1. A sketch of the motor response curve and the dependence of the up-gradient chemotactic velocity on the running time.

The curve represented in the main panel is a cartoon version of the clockwise (CW) bias vs the concentration of the second messenger CheYp of the chemotaxis pathway. Having the system set at the inflection point of the curve (blue point) would maximize the slope, i.e. the absolute sensitivity of the motor. However, the bacterial up-gradient velocity is not simply proportional to the absolute sensitivity, as discussed in the text. In particular, extending the duration of the runs can speed up the velocity as shown in the inset: the running time is reported in seconds on the abscissae while the solid line is Eq (4) with λ = 1 and the dashed line is again Eq (4) but λ changes now with τ_r so as to maximize the chemotactic velocity. The upshot is that points on the motor curve which do not maximize the absolute sensitivity, like the red one, can actually yield larger up-gradient speeds.

Fig 2. Variation of the bacterial running time with respect to the chemoattractant concentrations.

The curves refer to different concentrations of serine (red), aspartate (blue) or aspartate with a background of 30μM of serine (green). Times are normalized to the average running time (whence a non-dimensional quantity on the y-axis) in the absence of any chemoattractant, whose average over the bacterial population is ≃1.15s. Run times are calculated by averaging over at least three different experiments and error bars represent the error on the mean. The loss of precise adaptation for the green and the red curves is clearly visible. Note also that the value of the green curve at the lowest aspartate concentration is consistent with the value of the red curve at 30μM, as expected by the fact that the serine background becomes dominant.

Fig 3. The E. coli running speed vs the chemoattractant concentrations.

As in Fig 2, the three curves refer to serine (red), aspartate (blue) or aspartate with a background of 30μM of serine (green). The mean value is calculated by averaging over the population of bacteria and error bars represent the standard deviation of the velocity distribution over the population.

Fig 4. The experimental setup and raw images of bacteria running in the channels.

A. Illustration of the microfluidic setup where bacterial speed races take place. Reservoirs were filled with the appropriate concentration of chemoattractants and let diffuse through the lateral channels so as to establish linear gradients of chemoattractants in equilibrium with the flow of motility medium applied in the injection channel. Bacteria were then inserted into the injection channel and a fraction of them climb gradients of chemoattractants in the lateral channels. B. A typical stitched fluorescence image of a channel. A sequence of 20 images (exposure time of 200ms) were superimposed and then stitched together. On the extreme left, it is shown the injection channels, where the density of bacteria is the highest, while successive positions along the lateral channel are presented moving from the left to the right of the panel. C. A zoom of the images in panel B at diverse positions along the lateral channels.

Fig 5. The progression of bacteria in the lateral channels.

The graphs show at different times the so-called progression function, i.e. the distribution function of the number of bacteria cumulated from the position indicated on the abscissae up to the end of the channels on the side of the reservoirs. Curves were obtained using five different experiments. Panels A, B and C show the progression function for a gradient of aspartate, of serine, of aspartate with a background of serine, respectively. All the gradients go from 0 (at the entry of the channel) to 1mM.

Fig 6. The bacterial forefronts vs time.

We show the position of the (A) 10^th, (B) 20^th and (C) 40^th most advanced bacteria for a gradient of serine (red), a gradient of aspartate (blue) and a gradient of aspartate with a 30μM background of serine (green). Curves represent the mean of five experiments and error bars represent the error on the estimation of the mean.