Evaluation of rate law approximations in bottom-up kinetic models of metabolism

Abstract

Background: The mechanistic description of enzyme kinetics in a dynamic model of metabolism requires specifying the numerical values of a large number of kinetic parameters. The parameterization challenge is often addressed through the use of simplifying approximations to form reaction rate laws with reduced numbers of parameters. Whether such simplified models can reproduce dynamic characteristics of the full system is an important question.

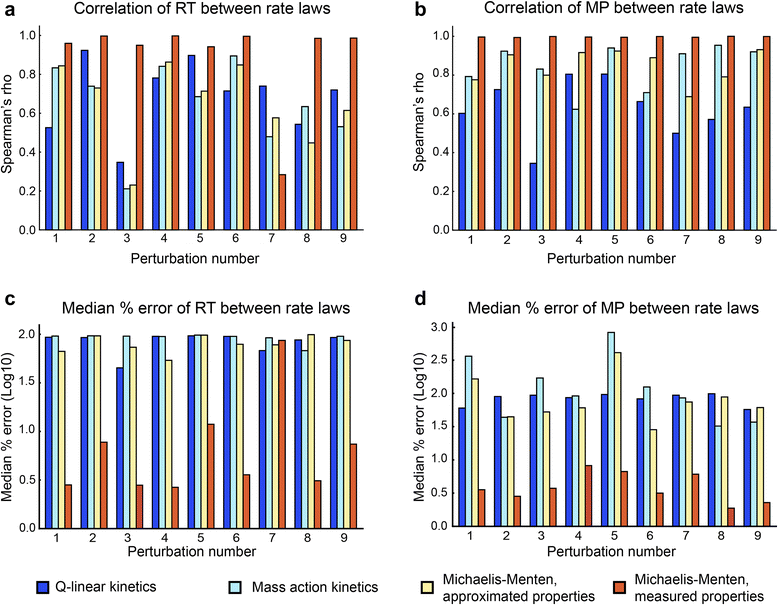
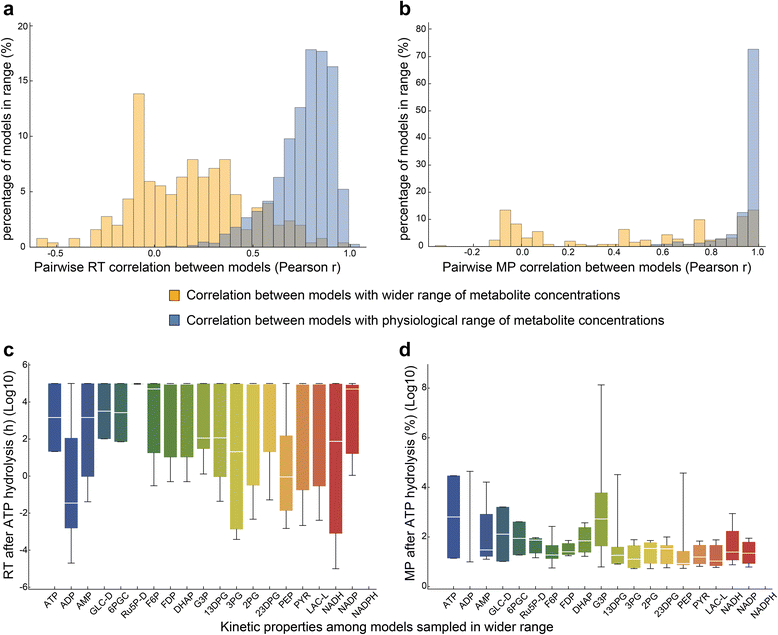
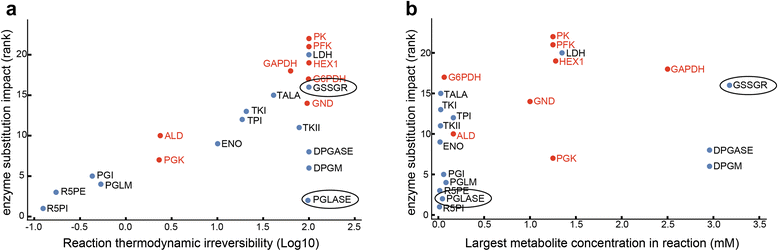
Results: In this work, we compared the local transient response properties of dynamic models constructed using rate laws with varying levels of approximation. These approximate rate laws were: 1) a Michaelis-Menten rate law with measured enzyme parameters, 2) a Michaelis-Menten rate law with approximated parameters, using the convenience kinetics convention, 3) a thermodynamic rate law resulting from a metabolite saturation assumption, and 4) a pure chemical reaction mass action rate law that removes the role of the enzyme from the reaction kinetics. We utilized in vivo data for the human red blood cell to compare the effect of rate law choices against the backdrop of physiological flux and concentration differences. We found that the Michaelis-Menten rate law with measured enzyme parameters yields an excellent approximation of the full system dynamics, while other assumptions cause greater discrepancies in system dynamic behavior. However, iteratively replacing mechanistic rate laws with approximations resulted in a model that retains a high correlation with the true model behavior. Investigating this consistency, we determined that the order of magnitude differences among fluxes and concentrations in the network were greatly influential on the network dynamics. We further identified reaction features such as thermodynamic reversibility, high substrate concentration, and lack of allosteric regulation, which make certain reactions more suitable for rate law approximations.

Conclusions: Overall, our work generally supports the use of approximate rate laws when building large scale kinetic models, due to the key role that physiologically meaningful flux and concentration ranges play in determining network dynamics. However, we also showed that detailed mechanistic models show a clear benefit in prediction accuracy when data is available. The work here should help to provide guidance to future kinetic modeling efforts on the choice of rate law and parameterization approaches.

Keywords: Approximate rate laws; Kinetic modeling; Mass action kinetics; Metabolic modeling; Michaelis-Menten kinetics.

Fig. 1

Comparison of rate laws and their resulting first derivatives. a Formulation of Michaelis-Menten kinetics with measured properties, Q-linear kinetics and Michaelis-Menten kinetics with approximated properties from the enzyme module with different layers of assumptions [42]. b Formulation of mass action kinetics based on the law of mass action for a pure chemical reaction. c First derivatives (reaction sensitivities) calculated from the four approximate rate laws. K _s and K _p are the Michaelis-Menten constants for the substrate and product. Γ is denoted as the mass-action ratio, which is the ratio of product concentrations over reactant concentrations in a steady state raised to the exponent of their stoichiometric coefficients. K _eq is the equilibrium constant of the reaction. k _cat ⁺ is the enzyme turnover rate constant. k ₊, as defined in MASS models, is the pseudo-elementary rate constant in the forward direction

Fig. 2

Schematic of the enzyme modules incorporated into the RBC metabolic network [33]. The ten modules constructed were primarily located in glycolysis and the pentose phosphate pathway. Other pathways were included as Q-linear kinetics approximations

Fig. 3

Simulation comparison of four simplified rate laws against a reference module containing detailed enzyme mechanism kinetics (enzyme modules). The responses of metabolites under different perturbations were compared between four simplified rate laws and the enzyme module. a Correlation of metabolite relaxation time. b Correlation of metabolite maximum perturbation. c Median percent errors of metabolite relaxation time. d Median percent errors of metabolite maximum perturbation. Nine different perturbations labeled from 1 to 9 were performed. 1, ATP, ADP and P_i perturbation; 2, NAD and NADH perturbation; 3, 23DPG perturbation; 4, 3PG perturbation; 5, PYR perturbation; 6, FDP perturbation; 7, PRPP perturbation; 8, MAN6P perturbation; 9, R5P perturbation. Spearman’s rho: Spearman’s rank correlation coefficient. The simulations were performed on the whole-cell kinetic model of erythrocyte constructed by Bordbar et al [33]

Fig. 4

Iterative replacement of Michaelis-Menten kinetics with measured properties by mass action kinetics. An increasing number of Michaelis-Menten kinetics rate laws with measured parameters were replaced by mass action kinetics, and the RT and MP of affected metabolites were calculated. The correlation of metabolite RT and MP between Michaelis-Menten kinetics and mass action kinetics fluctuated initially but gradually stabilized as more reactions were replaced with mass action kinetics. The black line is the average correlation of all nine perturbations performed. a Correlation of metabolite RTs between Michaelis-Menten and mass action model. b Correlation of metabolite MPs between Michaelis-Menten and mass action model. Spearman’s rho: Spearman’s rank correlation coefficient. The simulations were performed on the whole-cell kinetic model of erythrocyte constructed by Bordbar et al [33]

Fig. 5

Kinetic properties of models sampled with models sampled with physiological concentrations and fluxes compared to models sampled in wider ranges of concentrations and fluxes. First, 63 models were built with metabolite concentrations and fluxes sampled from physiologically relevant range. Then, 23 models were constructed with a wider range of metabolite concentrations (10⁻⁸ to 10⁵ mM) and fluxes. ATP hydrolysis was chosen as a reference perturbation as the perturbation on all models and RT and MP of the metabolites was calculated. a Distribution of pair-wise Pearson correlation coefficients of metabolite RTs for models sampled with wider concentration and flux ranges and models sampled with physiologically relevant ranges. b Distribution of pair-wise Pearson correlation coefficients of metabolite MPs for models sampled with wider concentration and flux ranges and models sampled with physiologically relevant ranges. c Distribution of metabolite RTs for models sampled with wider concentration and flux ranges. d Distribution of metabolite MPs for models sampled with wider concentration and flux ranges. The sampling and simulations were performed on the whole-cell kinetic model of erythrocyte constructed by Bordbar et al [33]

Fig. 6

Reaction properties affecting the impact of reaction rate law approximations. a Enzyme substitution impact (rank) against reaction thermodynamic irreversibility (Log10). Reaction thermodynamic irreversibility is calculated as (reaction equilibrium constant - mass action ratio)/reaction equilibrium constant. Lower rank score meant less change in dynamic response when the module is replaced by mass action kinetics. Reactions highlighted in red indicate presence of regulation. Circled reactions are outliers of the general trends. PGLASE is irreversible but shows low impact upon reaction rate law approximation. GSSGR has a large substrate concentration, yet still shows significant impact upon reaction rate law approximation. b Enzyme substitution impact (rank) against largest metabolite concentration in the reaction. Red and circled reactions are the same as in panel (a). The simulations were performed on the model constructed based on Mulquiney et al [34]