Bayesian inference with Stan: A tutorial on adding custom distributions
- PMID: 27287444
- PMCID: PMC5149118
- DOI: 10.3758/s13428-016-0746-9
Bayesian inference with Stan: A tutorial on adding custom distributions
Abstract
When evaluating cognitive models based on fits to observed data (or, really, any model that has free parameters), parameter estimation is critically important. Traditional techniques like hill climbing by minimizing or maximizing a fit statistic often result in point estimates. Bayesian approaches instead estimate parameters as posterior probability distributions, and thus naturally account for the uncertainty associated with parameter estimation; Bayesian approaches also offer powerful and principled methods for model comparison. Although software applications such as WinBUGS (Lunn, Thomas, Best, & Spiegelhalter, Statistics and Computing, 10, 325-337, 2000) and JAGS (Plummer, 2003) provide "turnkey"-style packages for Bayesian inference, they can be inefficient when dealing with models whose parameters are correlated, which is often the case for cognitive models, and they can impose significant technical barriers to adding custom distributions, which is often necessary when implementing cognitive models within a Bayesian framework. A recently developed software package called Stan (Stan Development Team, 2015) can solve both problems, as well as provide a turnkey solution to Bayesian inference. We present a tutorial on how to use Stan and how to add custom distributions to it, with an example using the linear ballistic accumulator model (Brown & Heathcote, Cognitive Psychology, 57, 153-178. doi: 10.1016/j.cogpsych.2007.12.002 , 2008).
Keywords: Bayesian inference; Linear ballistic accumulator; Probabilistic programming; Stan.
Figures



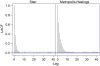
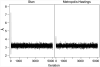
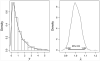
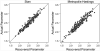


References
-
- Brooks S, Gelman A, Jones GL, Meng XL. Handbook of Markov chain Monte Carlo. Boca Raton, FL: Chapman & Hall/CRC; 2011.
-
- Duane S, Kennedy AD, Pendleton BJ, Roweth D. Hybrid Monte Carlo. Physics Letters B. 1987;195:216–222.
-
- Gelman A, Carlin JB, Stern HS, Dunson DB, Vehtari A, Rubin DB. Bayesian data analysis. 3rd. Boca Raton, FL: Chapman & Hall/CRC; 2013.
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

