Scalar utility theory and proportional processing: What does it actually imply?
- PMID: 27288541
- PMCID: PMC5683348
- DOI: 10.1016/j.jtbi.2016.06.003
Scalar utility theory and proportional processing: What does it actually imply?
Abstract
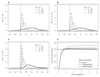
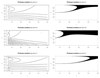
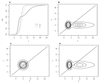
Scalar Utility Theory (SUT) is a model used to predict animal and human choice behaviour in the context of reward amount, delay to reward, and variability in these quantities (risk preferences). This article reviews and extends SUT, deriving novel predictions. We show that, contrary to what has been implied in the literature, (1) SUT can predict both risk averse and risk prone behaviour for both reward amounts and delays to reward depending on experimental parameters, (2) SUT implies violations of several concepts of rational behaviour (e.g. it violates strong stochastic transitivity and its equivalents, and leads to probability matching) and (3) SUT can predict, but does not always predict, a linear relationship between risk sensitivity in choices and coefficient of variation in the decision-making experiment. SUT derives from Scalar Expectancy Theory which models uncertainty in behavioural timing using a normal distribution. We show that the above conclusions also hold for other distributions, such as the inverse Gaussian distribution derived from drift-diffusion models. A straightforward way to test the key assumptions of SUT is suggested and possible extensions, future prospects and mechanistic underpinnings are discussed.
Keywords: Decision making; Risk preferences; Scalar expectancy theory; Scalar property; Weber's law.
Copyright © 2016 Elsevier Ltd. All rights reserved.
Conflict of interest statement
The authors declare no conflicting interests.
Figures
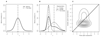
Similar articles
-
Framing effects and risky decisions in starlings.Proc Natl Acad Sci U S A. 2002 Mar 5;99(5):3352-5. doi: 10.1073/pnas.042491999. Epub 2002 Feb 26. Proc Natl Acad Sci U S A. 2002. PMID: 11867709 Free PMC article.
-
A temporal basis for Weber's law in value perception.Front Integr Neurosci. 2014 Oct 14;8:79. doi: 10.3389/fnint.2014.00079. eCollection 2014. Front Integr Neurosci. 2014. PMID: 25352791 Free PMC article.
-
Risk sensitivity for amounts of and delay to rewards: adaptation for uncertainty or by-product of reward rate maximising?Behav Processes. 2012 Feb;89(2):104-14. doi: 10.1016/j.beproc.2011.08.016. Epub 2011 Sep 15. Behav Processes. 2012. PMID: 21925575
-
Decision field theory: a dynamic-cognitive approach to decision making in an uncertain environment.Psychol Rev. 1993 Jul;100(3):432-59. doi: 10.1037/0033-295x.100.3.432. Psychol Rev. 1993. PMID: 8356185 Review.
-
Neurobiological studies of risk assessment: a comparison of expected utility and mean-variance approaches.Cogn Affect Behav Neurosci. 2008 Dec;8(4):363-74. doi: 10.3758/CABN.8.4.363. Cogn Affect Behav Neurosci. 2008. PMID: 19033235 Review.
Cited by
-
Principles of Economic Rationality in Mice.Sci Rep. 2017 Dec 12;7(1):17441. doi: 10.1038/s41598-017-17747-7. Sci Rep. 2017. PMID: 29234113 Free PMC article.
-
Bundling and segregation affect pheromone deposition, but not choice, in an ant.Elife. 2022 Nov 22;11:e79314. doi: 10.7554/eLife.79314. Elife. 2022. PMID: 36412093 Free PMC article.
-
Gains v. losses, or context dependence generated by confusion?Anim Cogn. 2020 Mar;23(2):361-366. doi: 10.1007/s10071-019-01339-1. Epub 2020 Jan 21. Anim Cogn. 2020. PMID: 31965401 Free PMC article.
-
Two-dimensional reward evaluation in mice.Anim Cogn. 2021 Sep;24(5):981-998. doi: 10.1007/s10071-021-01482-8. Epub 2021 Mar 15. Anim Cogn. 2021. PMID: 33721139 Free PMC article.
References
-
- Allan LG, Gibbon J. Human bisection at the geometric mean. Learning and Motivation. 1991;22(1–2):39–58. doi: 10.1016/0023-9690(91)90016-2. - DOI
-
- Barnard CJ, Brown CAJ, Houston AI, McNamara JM. Risk-sensitive foraging in common shrews: an interruption model and the effects of mean and variance in reward rate. Behavioral Ecology and Sociobiology. 1985;18(2):139–146.
-
- Bateson M, Kacelnik A. Accuracy of memory for amount in the foraging starling, Sturnus vulgaris. Animal Behaviour. 1995a;50(2):431–443. doi: 10.1006/anbe.1995.0257. - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

