Enhanced Spatial Resolution During Locomotion and Heightened Attention in Mouse Primary Visual Cortex
- PMID: 27307228
- PMCID: PMC4909779
- DOI: 10.1523/JNEUROSCI.0430-16.2016
Enhanced Spatial Resolution During Locomotion and Heightened Attention in Mouse Primary Visual Cortex
Abstract
We do not fully understand how behavioral state modulates the processing and transmission of sensory signals. Here, we studied the cortical representation of the retinal image in mice that spontaneously switched between a state of rest and a constricted pupil, and one of active locomotion and a dilated pupil, indicative of heightened attention. We measured the selectivity of neurons in primary visual cortex for orientation and spatial frequency, as well as their response gain, in these two behavioral states. Consistent with prior studies, we found that preferred orientation and spatial frequency remained invariant across states, whereas response gain increased during locomotion relative to rest. Surprisingly, relative gain, defined as the ratio between the gain during locomotion and the gain during rest, was not uniform across the population. Cells tuned to high spatial frequencies showed larger relative gain compared with those tuned to lower spatial frequencies. The preferential enhancement of high-spatial-frequency information was also reflected in our ability to decode the stimulus from population activity. Finally, we show that changes in gain originate from shifts in the operating point of neurons along a spiking nonlinearity as a function of behavioral state. Differences in the relative gain experienced by neurons with high and low spatial frequencies are due to corresponding differences in how these cells shift their operating points between behavioral states.
Significance statement: How behavioral state modulates the processing and transmission of sensory signals remains poorly understood. Here, we show that the mean firing rate and neuronal gain increase during locomotion as a result in a shift of the operating point of neurons. We define relative gain as the ratio between the gain of neurons during locomotion and rest. Interestingly, relative gain is higher in cells with preferences for higher spatial frequencies than those with low-spatial-frequency selectivity. This means that, during a state of locomotion and heightened attention, the population activity in primary visual cortex can support better spatial acuity, a phenomenon that parallels the improved spatial resolution observed in human subjects during the allocation of spatial attention.
Keywords: alertness; locomotion; neuronal gain; operating point; spatial acuity; visual cortex.
Copyright © 2016 the authors 0270-6474/16/366382-11$15.00/0.
Figures
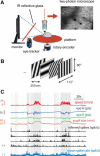

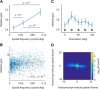
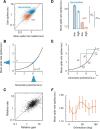
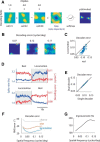
Comment in
-
How Attention Enhances Spatial Resolution: Preferential Gain Enhancement of High Spatial Frequency Neurons.J Neurosci. 2016 Nov 30;36(48):12080-12082. doi: 10.1523/JNEUROSCI.2691-16.2016. J Neurosci. 2016. PMID: 27903718 Free PMC article. No abstract available.
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
