An algorithm for computing the gene tree probability under the multispecies coalescent and its application in the inference of population tree

Abstract

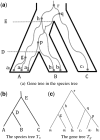
Motivation: Gene tree represents the evolutionary history of gene lineages that originate from multiple related populations. Under the multispecies coalescent model, lineages may coalesce outside the species (population) boundary. Given a species tree (with branch lengths), the gene tree probability is the probability of observing a specific gene tree topology under the multispecies coalescent model. There are two existing algorithms for computing the exact gene tree probability. The first algorithm is due to Degnan and Salter, where they enumerate all the so-called coalescent histories for the given species tree and the gene tree topology. Their algorithm runs in exponential time in the number of gene lineages in general. The second algorithm is the STELLS algorithm (2012), which is usually faster but also runs in exponential time in almost all the cases.

Results: In this article, we present a new algorithm, called CompactCH, for computing the exact gene tree probability. This new algorithm is based on the notion of compact coalescent histories: multiple coalescent histories are represented by a single compact coalescent history. The key advantage of our new algorithm is that it runs in polynomial time in the number of gene lineages if the number of populations is fixed to be a constant. The new algorithm is more efficient than the STELLS algorithm both in theory and in practice when the number of populations is small and there are multiple gene lineages from each population. As an application, we show that CompactCH can be applied in the inference of population tree (i.e. the population divergence history) from population haplotypes. Simulation results show that the CompactCH algorithm enables efficient and accurate inference of population trees with much more haplotypes than a previous approach.

Availability: The CompactCH algorithm is implemented in the STELLS software package, which is available for download at http://www.engr.uconn.edu/ywu/STELLS.html

Contact: ywu@engr.uconn.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

Fig. 1.

A gene tree (in thin lines) in the species tree (in thick lines) shown in (a). Gene lineages a₁, a₂ and a₃ originate from species A, b₁ and b₂ from B and c₁ from C. The species tree T_s is shown separately in (b), so is the gene tree T_g in (c). Internal nodes of both T_g and T_s are labeled. Coalescents: internal nodes of T_g. Branches of trees are represented by their lower nodes

Fig. 2.

The inferred population tree from ten populations in the 1000 Genomes Project using 20 haplotypes from then individual per population. Branch length shown is the estimated time in coalescent units