Random-phase metasurfaces at optical wavelengths
- PMID: 27328635
- PMCID: PMC4916468
- DOI: 10.1038/srep28448
Random-phase metasurfaces at optical wavelengths
Abstract
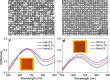
Random-phase metasurfaces, in which the constituents scatter light with random phases, have the property that an incident plane wave will diffusely scatter, hereby leading to a complex far-field response that is most suitably described by statistical means. In this work, we present and exemplify the statistical description of the far-field response, particularly highlighting how the response for polarised and unpolarised light might be alike or different depending on the correlation of scattering phases for two orthogonal polarisations. By utilizing gap plasmon-based metasurfaces, consisting of an optically thick gold film overlaid by a subwavelength thin glass spacer and an array of gold nanobricks, we design and realize random-phase metasurfaces at a wavelength of 800 nm. Optical characterisation of the fabricated samples convincingly demonstrates the diffuse scattering of reflected light, with statistics obeying the theoretical predictions. We foresee the use of random-phase metasurfaces for camouflage applications and as high-quality reference structures in dark-field microscopy, while the control of the statistics for polarised and unpolarised light might find usage in security applications. Finally, by incorporating a certain correlation between scattering by neighbouring metasurface constituents new types of functionalities can be realised, such as a Lambertian reflector.
Figures


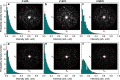
 ] and described by equation (3); (d) unpolarised incident light when both ϕx and ϕy are described by equation (3) but are statistically independent. The histogram plots show the PDF of the calculated far-field intensity in the upper half-space within an NA of 0.9, while the red lines correspond to the theoretical predictions by equations (5) and (6). The insets show the associated Fourier images of the far-field intensities within the NA = 0.9.
] and described by equation (3); (d) unpolarised incident light when both ϕx and ϕy are described by equation (3) but are statistically independent. The histogram plots show the PDF of the calculated far-field intensity in the upper half-space within an NA of 0.9, while the red lines correspond to the theoretical predictions by equations (5) and (6). The insets show the associated Fourier images of the far-field intensities within the NA = 0.9.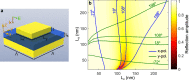

References
-
- Pendry J. B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 85, 3966–3969 (2000). - PubMed
-
- Shelby R. A., Smith D. R. & Schultz S. Experimental verification of a negative index of refraction. Science 292, 77–79 (2001). - PubMed
-
- Pendry J. B., Schurig D. & Smith D. R. Controlling electromagnetic fields. Science 312, 1780–1782 (2006). - PubMed
-
- Schurig D. et al. Metamaterial electromagnetic cloak at microwave frequencies. Science 314, 977–980 (2006). - PubMed
-
- Fang N., Lee H., Sun C. & Zhang X. Sub–diffraction-limited optical imaging with a silver superlens. Science 308, 534–537 (2005). - PubMed
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

