Methods to Assess Measurement Error in Questionnaires of Sedentary Behavior

Abstract

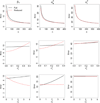
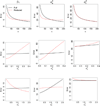
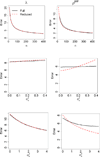
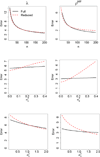
Sedentary behavior has already been associated with mortality, cardiovascular disease, and cancer. Questionnaires are an affordable tool for measuring sedentary behavior in large epidemiological studies. Here, we introduce and evaluate two statistical methods for quantifying measurement error in questionnaires. Accurate estimates are needed for assessing questionnaire quality. The two methods would be applied to validation studies that measure a sedentary behavior by both questionnaire and accelerometer on multiple days. The first method fits a reduced model by assuming the accelerometer is without error, while the second method fits a more complete model that allows both measures to have error. Because accelerometers tend to be highly accurate, we show that ignoring the accelerometer's measurement error, can result in more accurate estimates of measurement error in some scenarios. In this manuscript, we derive asymptotic approximations for the Mean-Squared Error of the estimated parameters from both methods, evaluate their dependence on study design and behavior characteristics, and offer an R package so investigators can make an informed choice between the two methods. We demonstrate the difference between the two methods in a recent validation study comparing Previous Day Recalls (PDR) to an accelerometer-based ActivPal.

Keywords: PDR; measurement error; questionnaire; sedentary.

Figure 1

(large-error scenario): The % error (y axis), defined to be the square-root of the Mean Square Error divided by the parameter value, for estimates of β₁ (1^st column), ${\sigma }_{\epsilon }^2$ (2^nd column), and ${\sigma }_r^2$ (3^rd column), as a function of changing n (number of subjects, 1^st row), ${\sigma }_u^2$ (variance of gold standard, 2^nd row), and ${\sigma }_{\delta }^2$ (intra-individual variability, 3^rd row). The % error for estimates based on the full model are unbroken black lines, while the % error for estimates based on the reduced model are broken red lines. The evaluated scenario assumes N=4 measures per individual, an independence correlation matrix, and with the exception of the variable being changed, we let n=50, ${\beta }_1=1,{\sigma }_T^2=4,{\sigma }_{\delta }^2=1.5,{\sigma }_U^2=0.1,4.0$, and ${\sigma }_r^2=0.8$

Figure 2

(small error scenario): The % error (y axis), defined to be the square-root of the Mean Square Error divided by the parameter value, for estimates of β₁ (1^st column), ${\sigma }_{\epsilon }^2$ (2^nd column), and ${\sigma }_r^2$ (3^rd column), as a function of changing n (number of subjects, 1^st row), ${\sigma }_u^2$ (variance of gold standard, 2^nd row), and ${\sigma }_{\delta }^2$ (intra-individual variability, 3^rd row). The % error for estimates based on the full model are unbroken black lines, while the % error for estimates based on the reduced model are broken red lines. The evaluated scenario assumes N=4 measures per individual, an independence correlation matrix, and with the exception of the variable being changed, we let n=50, ${\beta }_1=1,{\sigma }_T^2=4,{\sigma }_{\delta }^2=1.5,{\sigma }_U^2=0.1,{\sigma }_{\epsilon }^2=0.5$, and ${\sigma }_r^2=0.8$

Figure 3

(large error scenario): The % error (y axis), defined to be the square-root of the Mean Square Error divided by the parameter value, for estimates of λ (1^st column) and ρ^PDR (2^rd column), as a function of changing n (number of subjects, 1^st row), ${\sigma }_u^2$ (variance of gold standard, 2^nd row), and ${\sigma }_{\delta }^2$ (intra-individual variability, 3^rd row). The % error for estimates based on the full model are unbroken black lines, while the % error for estimates based on the reduced model are broken red lines. The evaluated scenario assumes N=4 measures per individual, an independence correlation matrix, and with the exception of the variable being changed, we let n=50, ${\beta }_1=1,{\sigma }_T^2=4,{\sigma }_{\delta }^2=1.5,{\sigma }_U^2=0.1,{\sigma }_{\epsilon }^2=4$, and ${\sigma }_r^2=0.8$

Figure 4

(small error scenario): The % error (y axis), defined to be the square-root of the Mean Square Error divided by the parameter value, for estimates of λ (1^st column) and ρ^PDR (2^rd column), as a function of changing n (number of subjects, 1^st row), ${\sigma }_u^2$ (variance of gold standard, 2^nd row), and ${\sigma }_{\delta }^2$ (intra-individual variability, 3^rd row). The % error for estimates based on the full model are unbroken black lines, while the % error for estimates based on the reduced model are broken red lines. The evaluated scenario assumes N=4 measures per individual, an independence correlation matrix, and with the exception of the variable being changed, we let n=50, ${\beta }_1=1,{\sigma }_T^2=4,{\sigma }_{\delta }^2=1.5,{\sigma }_U^2=0.1,{\sigma }_{\epsilon }^2=0.5$, and ${\sigma }_r^2=0.8$