Muscle shortening velocity depends on tissue inertia and level of activation during submaximal contractions
- PMID: 27354711
- PMCID: PMC4938035
- DOI: 10.1098/rsbl.2015.1041
Muscle shortening velocity depends on tissue inertia and level of activation during submaximal contractions
Abstract
In order to perform external work, muscles must do additional internal work to deform their tissue, and in particular, to overcome the inertia due to their internal mass. However, the contribution of the internal mass within a muscle to the mechanical output of that muscle has only rarely been studied. Here, we use a dynamic, multi-element Hill-type muscle model to examine the effects of the inertial mass within muscle on its contractile performance. We find that the maximum strain-rate of muscle is slower for lower activations and larger muscle sizes. As muscle size increases, the ability of the muscle to overcome its inertial load will decrease, as muscle tension is proportional to cross-sectional area and inertial load is proportional to mass. Thus, muscles that are larger in size will have a higher inertial cost to contraction. Similarly, when muscle size and inertial load are held constant, decreasing muscle activation will increase inertial cost to contraction by reducing muscle tension. These results show that inertial loads within muscle contribute to a slowing of muscle contractile velocities (strain-rates), particularly at the submaximal activations that are typical during animal locomotion.
Keywords: activation; contractile velocity; inertia; modelling; muscle mechanics.
© 2016 The Author(s).
Figures

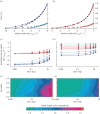
 achieved at 0.01F0 with no external load (c) and the strain-rate achieved at 0.15F0 with an added external load of 0.6M (d) are shown for a range from maximal (solid lines) through to 20% activation (shortest dashes). Note the similar strain-rates for fast and slow muscles at 20 and 30% activation (open circles), respectively, representing data from Holt et al. [12]. Fast muscle is shown in blue and slow muscle in red for (a–d). The initial lengths required to achieve
achieved at 0.01F0 with no external load (c) and the strain-rate achieved at 0.15F0 with an added external load of 0.6M (d) are shown for a range from maximal (solid lines) through to 20% activation (shortest dashes). Note the similar strain-rates for fast and slow muscles at 20 and 30% activation (open circles), respectively, representing data from Holt et al. [12]. Fast muscle is shown in blue and slow muscle in red for (a–d). The initial lengths required to achieve  at L0 are shown as a function of muscle mass and activation for the fast (e) and slow (f) muscle for simulation-II.
at L0 are shown as a function of muscle mass and activation for the fast (e) and slow (f) muscle for simulation-II.Similar articles
-
Size, History-Dependent, Activation and Three-Dimensional Effects on the Work and Power Produced During Cyclic Muscle Contractions.Integr Comp Biol. 2018 Aug 1;58(2):232-250. doi: 10.1093/icb/icy021. Integr Comp Biol. 2018. PMID: 29726964 Free PMC article.
-
A modelling approach for exploring muscle dynamics during cyclic contractions.PLoS Comput Biol. 2018 Apr 16;14(4):e1006123. doi: 10.1371/journal.pcbi.1006123. eCollection 2018 Apr. PLoS Comput Biol. 2018. PMID: 29659583 Free PMC article.
-
Probing the limits to muscle-powered accelerations: lessons from jumping bullfrogs.J Exp Biol. 2003 Aug;206(Pt 15):2567-80. doi: 10.1242/jeb.00452. J Exp Biol. 2003. PMID: 12819264
-
How muscles deal with real-world loads: the influence of length trajectory on muscle performance.J Exp Biol. 1999 Dec;202(Pt 23):3377-85. doi: 10.1242/jeb.202.23.3377. J Exp Biol. 1999. PMID: 10562520 Review.
-
Disproportionate changes in skeletal muscle strength and size with resistance training and ageing.J Musculoskelet Neuronal Interact. 2009 Jul-Sep;9(3):123-9. J Musculoskelet Neuronal Interact. 2009. PMID: 19724146 Review.
Cited by
-
The Energy of Muscle Contraction. I. Tissue Force and Deformation During Fixed-End Contractions.Front Physiol. 2020 Aug 31;11:813. doi: 10.3389/fphys.2020.00813. eCollection 2020. Front Physiol. 2020. PMID: 32982762 Free PMC article.
-
The energy of muscle contraction. IV. Greater mass of larger muscles decreases contraction efficiency.J R Soc Interface. 2021 Sep;18(182):20210484. doi: 10.1098/rsif.2021.0484. Epub 2021 Sep 29. J R Soc Interface. 2021. PMID: 34583567 Free PMC article.
-
Added mass in rat plantaris muscle causes a reduction in mechanical work.J Exp Biol. 2020 Oct 7;223(Pt 19):jeb224410. doi: 10.1242/jeb.224410. J Exp Biol. 2020. PMID: 32737211 Free PMC article.
-
Muscle-spring dynamics in time-limited, elastic movements.Proc Biol Sci. 2016 Sep 14;283(1838):20161561. doi: 10.1098/rspb.2016.1561. Proc Biol Sci. 2016. PMID: 27629031 Free PMC article.
-
Size, History-Dependent, Activation and Three-Dimensional Effects on the Work and Power Produced During Cyclic Muscle Contractions.Integr Comp Biol. 2018 Aug 1;58(2):232-250. doi: 10.1093/icb/icy021. Integr Comp Biol. 2018. PMID: 29726964 Free PMC article.
References
-
- Marsh RL, Bennett AF. 1986. Thermal-dependence of contractile properties of skeletal-muscle from the lizard Sceloporus occidentalis with comments on methods for fitting and comparing force–velocity curves. J. Exp. Biol. 126, 63–77. - PubMed
-
- Askew GN, Marsh RL. 1997. The effects of length trajectory on the mechanical power output of mouse skeletal muscles. J. Exp. Biol. 200, 3119–3131. - PubMed
Publication types
MeSH terms
Associated data
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

