Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2004 Apr 1;109(2):267-77.
doi: 10.6028/jres.109.017. Print 2004 Mar-Apr.

Simulation of Sheared Suspensions With a Parallel Implementation of QDPD

James S Sims  1 , Nicos Martys  1
Affiliations

Simulation of Sheared Suspensions With a Parallel Implementation of QDPD

James S Sims et al. J Res Natl Inst Stand Technol. .

Abstract

A parallel quaternion-based dissipative particle dynamics (QDPD) program has been developed in Fortran to study the flow properties of complex fluids subject to shear. The parallelization allows for simulations of greater size and complexity and is accomplished with a parallel link-cell spatial (domain) decomposition using MPI. The technique has novel features arising from the DPD formalism, the use of rigid body inclusions spread across processors, and a sheared boundary condition. A detailed discussion of our implementation is presented, along with results on two distributed memory architectures. A parallel speedup of 24.19 was obtained for a benchmark calculation on 27 processors of a distributed memory cluster.

Keywords: dissipative particle dynamics; domain decomposition; mesoscopic modeling; parallel algorithms; rheology; spatial decomposition; suspensions.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
Schematic diagram of link-cell algorithm for a two dimensional system (after Tildesley, Pinches, and Smith [11]).
Fig. 2
Fig. 2
Schematic 2-D representation of the link-cell algorithm.
Fig. 3
Fig. 3
Tumbling of a single ellipsoidal inclusion under shear. Details of the algorithm for a rigid body are given in [5].
Fig. 4
Fig. 4
Lees-Edwards boundary conditions for homogeneous shear (adopted from Allen and Tildesley, Computer Simulation of Liquids, Oxford, 1987, Fig. 8.2).
Fig. 5
Fig. 5
A 9 processor 2-D domain. The small rectangles are cells associated with the link-cell algorithm. The dashed lines correspond to the ghost cells.
Fig. 6
Fig. 6
Enlargement of the central region of Figure 5. Link-cell periodic boundaries become processor domain boundaries. Dashed lines correspond to ghost cells.
Fig. 7
Fig. 7
A 2-D example of the parallel link-cell algorithm showing a processor containing cells on the edge of the simulation box.
Fig. 8
Fig. 8
A nine processor 2-D domain decomposition and neighboring layers resulting from application of an applied strain consistent with the Lees-Edwards boundary condition.
Fig. 9
Fig. 9
A more detailed nine processor 2-D domain decomposition including shear.
Fig. 10
Fig. 10
Logarithm (base e) of normalized CPU time (seconds) versus number of processors. The performance of the replicated data version degrades much more quickly than the spatial decomposition version of the same code.
See this image and copyright information in PMC

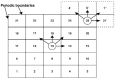
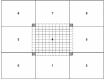
References

    1. Hoogerbrugge PJ, Koelman JMVA. Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics. Europhys Lett. 1992;19(1):155.
    1. Español P, Warren P. Statistical mechanics of dissipative particle dynamics. Europhys Lett. 1995;30:191.
    1. Marsh C, Backx G, Ernst MH. The Fokker-Planck-Boltzmann equation for dissipative particle dynamics. Europhys Lett. 1997;38:441.
    1. Martys NS, Mountain RD. Velocity Verlet algorithm for dissipative-particle-based models of suspensions. Phys Rev E. 1999;59(3):3733.
    1. Verlet L. Computer “experiments” on classical fluids. I. thermodynamical properties of lennard-jones molecules. Phys Rev. 1967;165:201.

LinkOut - more resources