Modeling confounding by half-sibling regression
- PMID: 27382154
- PMCID: PMC4941423
- DOI: 10.1073/pnas.1511656113
Modeling confounding by half-sibling regression
Abstract
We describe a method for removing the effect of confounders to reconstruct a latent quantity of interest. The method, referred to as "half-sibling regression," is inspired by recent work in causal inference using additive noise models. We provide a theoretical justification, discussing both independent and identically distributed as well as time series data, respectively, and illustrate the potential of the method in a challenging astronomy application.
Keywords: astronomy; causal inference; exoplanet detection; machine learning; systematic error modeling.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
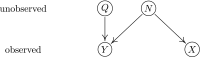
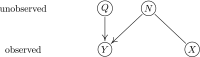
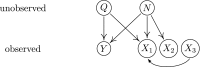
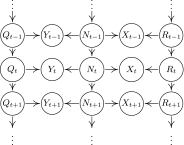
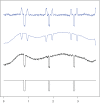
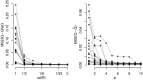


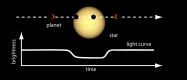

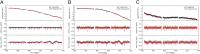
References
-
- Schölkopf B, et al. On causal and anticausal learning. In: Langford J, Pineau J, editors. Proceedings of the 29th International Conference on Machine Learning (ICML) Omnipress; New York: 2012. pp. 1255–1262.
-
- Pearl J. Causality. Cambridge Univ Press; New York: 2000.
-
- Spirtes P, Glymour C, Scheines R. Causation, Prediction, and Search. 2nd Ed MIT Press; Cambridge, MA: 1993.
-
- Aldrich J. Autonomy. Oxf Econ Pap. 1989;41(1):15–34.
-
- Hoover KD. Causality in economics and econometrics. In: Durlauf SN, Blume LE, editors. Economics and Philosophy. 2nd Ed. Vol 6 Palgrave Macmillan; New York: 2008.
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

