An inverse approach to determining spatially varying arterial compliance using ultrasound imaging
- PMID: 27384105
- PMCID: PMC5111829
- DOI: 10.1088/0031-9155/61/15/5486
An inverse approach to determining spatially varying arterial compliance using ultrasound imaging
Abstract
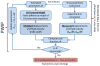
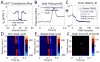
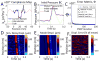
The mechanical properties of arteries are implicated in a wide variety of cardiovascular diseases, many of which are expected to involve a strong spatial variation in properties that can be depicted by diagnostic imaging. A pulse wave inverse problem (PWIP) is presented, which can produce spatially resolved estimates of vessel compliance from ultrasound measurements of the vessel wall displacements. The 1D equations governing pulse wave propagation in a flexible tube are parameterized by the spatially varying properties, discrete cosine transform components of the inlet pressure boundary conditions, viscous loss constant and a resistance outlet boundary condition. Gradient descent optimization is used to fit displacements from the model to the measured data by updating the model parameters. Inversion of simulated data showed that the PWIP can accurately recover the correct compliance distribution and inlet pressure under realistic conditions, even under high simulated measurement noise conditions. Silicone phantoms with known compliance contrast were imaged with a clinical ultrasound system. The PWIP produced spatially and quantitatively accurate maps of the phantom compliance compared to independent static property estimates, and the known locations of stiff inclusions (which were as small as 7 mm). The PWIP is necessary for these phantom experiments as the spatiotemporal resolution, measurement noise and compliance contrast does not allow accurate tracking of the pulse wave velocity using traditional approaches (e.g. 50% upstroke markers). Results from simulations indicate reflections generated from material interfaces may negatively affect wave velocity estimates, whereas these reflections are accounted for in the PWIP and do not cause problems.
Figures



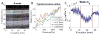
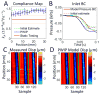
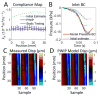
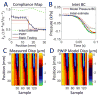
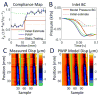
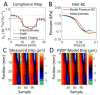
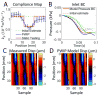
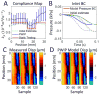
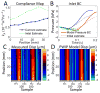
Similar articles
-
In vivo repeatability of the pulse wave inverse problem in human carotid arteries.J Biomech. 2017 Nov 7;64:136-144. doi: 10.1016/j.jbiomech.2017.09.017. Epub 2017 Sep 27. J Biomech. 2017. PMID: 29050824 Free PMC article.
-
A simulation environment for validating ultrasonic blood flow and vessel wall imaging based on fluid-structure interaction simulations: ultrasonic assessment of arterial distension and wall shear rate.Med Phys. 2010 Aug;37(8):4318-30. doi: 10.1118/1.3462592. Med Phys. 2010. PMID: 20879592
-
Cross-correlation analysis of pulse wave propagation in arteries: in vitro validation and in vivo feasibility.Phys Med Biol. 2018 May 29;63(11):115006. doi: 10.1088/1361-6560/aabe57. Phys Med Biol. 2018. PMID: 29658889 Free PMC article.
-
Mechanical events within the arterial wall under the forces of pulsatile flow: a review.J Mech Behav Biomed Mater. 2011 Nov;4(8):1595-602. doi: 10.1016/j.jmbbm.2011.01.005. Epub 2011 Jan 28. J Mech Behav Biomed Mater. 2011. PMID: 22098861 Review.
-
Arterial wall elasticity: state of the art and future prospects.Diagn Interv Imaging. 2013 May;94(5):561-9. doi: 10.1016/j.diii.2013.01.025. Epub 2013 Apr 22. Diagn Interv Imaging. 2013. PMID: 23619291 Review.
Cited by
-
An analytical model of full-field displacement and strain induced by amplitude-modulated focused ultrasound in harmonic motion imaging.Phys Med Biol. 2021 Apr 6;66(7):10.1088/1361-6560/abddd1. doi: 10.1088/1361-6560/abddd1. Phys Med Biol. 2021. PMID: 33472178 Free PMC article.
-
Feasibility and Validation of 4-D Pulse Wave Imaging in Phantoms and In Vivo.IEEE Trans Ultrason Ferroelectr Freq Control. 2017 Sep;64(9):1305-1317. doi: 10.1109/TUFFC.2017.2735381. Epub 2017 Aug 3. IEEE Trans Ultrason Ferroelectr Freq Control. 2017. PMID: 28792891 Free PMC article.
-
Pulse Wave Imaging Coupled With Vector Flow Mapping: A Phantom, Simulation, and In Vivo Study.IEEE Trans Ultrason Ferroelectr Freq Control. 2021 Jul;68(7):2516-2531. doi: 10.1109/TUFFC.2021.3074113. Epub 2021 Jun 29. IEEE Trans Ultrason Ferroelectr Freq Control. 2021. PMID: 33950838 Free PMC article.
-
Effect of Local Neck Anatomy on Localized One-Dimensional Measurements of Arterial Stiffness: A Finite-Element Model Study.J Biomech Eng. 2019 Mar 1;141(3):0310111-9. doi: 10.1115/1.4042435. J Biomech Eng. 2019. PMID: 30702744 Free PMC article.
-
Pulse wave imaging using coherent compounding in a phantom and in vivo.Phys Med Biol. 2017 Mar 7;62(5):1700-1730. doi: 10.1088/1361-6560/aa553a. Epub 2016 Dec 21. Phys Med Biol. 2017. PMID: 28002039 Free PMC article.
References
-
- Asmar R, Benetos A, Topouchian J, Laurent P, Pannier B, Brisac A, … Levy B. Assessment of arterial distensibility by automatic pulse wave velocity measurement: validation and clinical application studies. Hypertension. 1995;26(3):485–490. - PubMed
-
- Blacher J, Asmar R, Djane S, London G, Safar M. Aortic pulse wave velocity as a marker of cardiovascular risk in hypertensive patients. Hypertension. 1999;33(5):1111–1117. - PubMed
-
- Brekken R, Bang J, Ødegård A, Aasland J, Hernes T, Myhre H. Strain estimation in abdominal aortic aneurysms from 2-D ultrasound. Ultrasound in medicine & biology. 2006;32(1):33–42. - PubMed
-
- Chen C, Nevo E, Fetics B, Pak P, Yin F, Maughan W, Kass D. Estimation of central aortic pressure waveform by mathematical transformation of radial tonometry pressure validation of generalized transfer function. Circulation. 1997;95(7):1827–1836. - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
