Measurement of a vacuum-induced geometric phase

Abstract

Berry's geometric phase naturally appears when a quantum system is driven by an external field whose parameters are slowly and cyclically changed. A variation in the coupling between the system and the external field can also give rise to a geometric phase, even when the field is in the vacuum state or any other Fock state. We demonstrate the appearance of a vacuum-induced Berry phase in an artificial atom, a superconducting transmon, interacting with a single mode of a microwave cavity. As we vary the phase of the interaction, the artificial atom acquires a geometric phase determined by the path traced out in the combined Hilbert space of the atom and the quantum field. Our ability to control this phase opens new possibilities for the geometric manipulation of atom-cavity systems also in the context of quantum information processing.

Keywords: Berry phase; circuit-QED; transmon; vacuum fluctuations.

Fig. 1. Berry phase induced by a quantized field.

(A) An atomic transition between two states, |g〉 and |f〉, is driven by a coherent tone of amplitude α, phase ϕ, and detuning Δ. The phase ϕ is slowly varied between 0 and 2π. (B) In a frame rotating at the drive frequency, the drive acts as an effective magnetic field (red thick arrow) precessing around the ẑ axis. In the adiabatic limit, the Bloch vector stays aligned with the field and describes a circular path on the Bloch sphere spanned by the atomic basis states |g〉 and |f〉. The acquired geometric phase equals half the solid angle Ω subtended by the path. (C) By placing the atom in a cavity, the atom interacts with a quantized field. The interaction between the atom and the field is controlled by a microwave-activated coupling, which is mediated by an intermediate state |e〉 and is tunable in amplitude g and phase ϕ. (D) Admissible paths on the Bloch sphere for different numbers of photons n in the cavity. For each n, the Bloch sphere is spanned by the basis states |g, n + 1〉 and |f, n〉 of the combined atom-cavity system.

Fig. 2. Transmon in a 3D cavity with mode-selective coupling ports.

(A) Edited photograph of the 3D cavity used in the experiment. Two sapphire chips are placed inside the cavity. A transmon is patterned on the left chip (blue circle). (B) Cross section of the electric field magnitude |$\overrightarrow{\mathit{E}}$| for the two lowest-frequency modes of the cavity in (A), as obtained from a finite-element simulation. The chip used in the experiment is highlighted in blue, and the cavity ports are indicated as circles (not drawn to scale). (C) Diagram of the relevant frequencies for the experiment: first three cavity modes, ω₁, ω₂, and ω₃ (red), first two transitions of the transmon, ω_ge and ω_ef (blue), and higher-order transition between states |f0〉 and |g1〉, ω_d (yellow).

Fig. 3. Vacuum-induced Berry phase: Resonant case.

(A) Pulse sequence to detect the geometric phase acquired by the state $|{\mathrm{\Psi }}_{\mathit{n}}^{-}\rangle$ for resonant coupling (Δ = 0). The cavity is prepared in an n-photon Fock state by repeating the initial sequence n times. The system is prepared in a superposition of |e, n〉 and $|{\mathrm{\Psi }}_{\mathit{n}}^{-}\rangle$. Then, the resonant coupling is turned on, and its phase is increased by 2π during a time τ. Finally, the relative phase between $|{\mathrm{\Psi }}_{\mathit{n}}^{-}\rangle$ and |e, n〉 is determined by Ramsey interferometry. (B) Oscillations observed in the e-state population P_e when varying the phase ϕ_R of the second Ramsey pulse, with τ = 420 ns and n = 0. 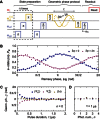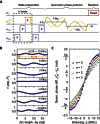The measurement described in (A) (δϕ = 2π; dark magenta squares) is compared against a reference measurement in which the phase of the coupling is held fixed (δϕ = 0; blue circles). The phase shift observed in the Ramsey pattern corresponds to an accumulated geometric phase ${\mathrm{\gamma }}_0^{-}$ = (3.13 ± 0.06). (C) Geometric phase γ, determined as in (B), versus pulse duration τ. Three different states are prepared: the two eigenstates, $|{\mathrm{\Psi }}_0^{-}\rangle$ (blue circles) and $|{\mathrm{\Psi }}_0^{+}\rangle$ (dark magenta squares), and the state |f0〉 (yellow diamonds), for which the cavity is initially in the vacuum state. (D) Geometric phase accumulated by the states $|{\mathrm{\Psi }}_{\mathit{n}}^{\pm }\rangle$ and |f, n〉, with fixed pulse duration τ and varying photon number n.

Fig. 4. Vacuum-induced Berry phase: Finite detuning.

(A) Pulse sequence to detect the geometric phase difference accumulated between states $|{\mathrm{\Psi }}_{\mathit{n}}^{-}\rangle$ and $|{\mathrm{\Psi }}_{\mathit{n}}^{+}\rangle$ at finite detuning Δ. We first prepare the state |f, n〉, which is a superposition of $|{\mathrm{\Psi }}_{\mathit{n}}^{-}\rangle$ and $|{\mathrm{\Psi }}_{\mathit{n}}^{+}\rangle$. Then, we turn on the coupling and vary its phase by an amount δϕ. We repeat this operation twice, the second time with an opposite detuning −Δ, an opposite phase variation −δϕ, and a π phase shift. This sequence results in dynamic phase cancellation, whereas the different geometric phases accumulated by $|{\mathrm{\Psi }}_{\mathit{n}}^{\pm }\rangle$ can be detected as a population transfer away from the state |f, n〉. (B) Oscillations in the f-state population P_f as a function of the phase displacement δϕ, for selected values of the detuning Δ (circles, data; solid lines, sine fit) and n = 0 photons in the cavity. The phase of the oscillations when δϕ = 2π corresponds to the accumulated geometric phase in a single closed loop (whose extent is indicated by an orange line). (C) Geometric phase difference, $({\mathrm{\gamma }}_{\mathit{n}}^{+}-{\mathrm{\gamma }}_{\mathit{n}}^{-})$, versus detuning Δ for different photon numbers n (symbols). The solid lines are a simultaneous fit of the model expression (Eq. 2) to all data sets, with the coupling constant g as the only fit parameter.