Toward a More Efficient Implementation of Antifibrillation Pacing
- PMID: 27391010
- PMCID: PMC4938213
- DOI: 10.1371/journal.pone.0158239
Toward a More Efficient Implementation of Antifibrillation Pacing
Abstract
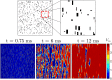
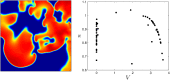
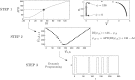
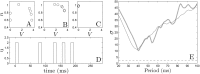
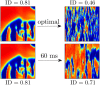
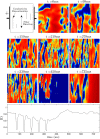
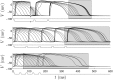
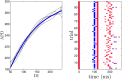
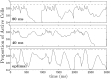
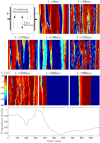
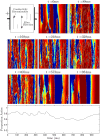
We devise a methodology to determine an optimal pattern of inputs to synchronize firing patterns of cardiac cells which only requires the ability to measure action potential durations in individual cells. In numerical bidomain simulations, the resulting synchronizing inputs are shown to terminate spiral waves with a higher probability than comparable inputs that do not synchronize the cells as strongly. These results suggest that designing stimuli which promote synchronization in cardiac tissue could improve the success rate of defibrillation, and point towards novel strategies for optimizing antifibrillation pacing.
Conflict of interest statement
Figures


Similar articles
-
Turbulence control with local pacing and its implication in cardiac defibrillation.Chaos. 2007 Mar;17(1):015107. doi: 10.1063/1.2713688. Chaos. 2007. PMID: 17411264 Review.
-
Low energy defibrillation in human cardiac tissue: a simulation study.Biophys J. 2009 Feb 18;96(4):1364-73. doi: 10.1016/j.bpj.2008.11.031. Biophys J. 2009. PMID: 19217854 Free PMC article.
-
European Resuscitation Council Guidelines for Resuscitation 2010 Section 3. Electrical therapies: automated external defibrillators, defibrillation, cardioversion and pacing.Resuscitation. 2010 Oct;81(10):1293-304. doi: 10.1016/j.resuscitation.2010.08.008. Resuscitation. 2010. PMID: 20956050 No abstract available.
-
Alternans and the influence of ionic channel modifications: Cardiac three-dimensional simulations and one-dimensional numerical bifurcation analysis.Chaos. 2007 Mar;17(1):015104. doi: 10.1063/1.2715668. Chaos. 2007. PMID: 17411261
-
Defibrillation of the heart: insights into mechanisms from modelling studies.Exp Physiol. 2006 Mar;91(2):323-37. doi: 10.1113/expphysiol.2005.030973. Epub 2006 Feb 9. Exp Physiol. 2006. PMID: 16469820 Review.
Cited by
-
Terminating spiral waves with a single designed stimulus: Teleportation as the mechanism for defibrillation.Proc Natl Acad Sci U S A. 2022 Jun 14;119(24):e2117568119. doi: 10.1073/pnas.2117568119. Epub 2022 Jun 9. Proc Natl Acad Sci U S A. 2022. PMID: 35679346 Free PMC article.
References
-
- Jacq F, Foulldrin G, Savouré A, Anselme F, Baguelin-Pinaud A, Cribier A, et al. A comparison of anxiety, depression and quality of life between device shock and nonshock groups in implantable cardioverter defibrillator recipients. General Hospital Psychiatry. 2009;31(3):266–273. 10.1016/j.genhosppsych.2009.01.003 - DOI - PubMed
-
- Suzuki T, Shiga T, Kuwahara K, Kobayashi S, Suzuki S, Nishimura K, et al. Prevalence and Persistence of Depression in Patients with Implantable Cardioverter Defibrillator: A 2-year Longitudinal Study. Pacing and Clinical Electrophysiology. 2010;33(12):1455–1461. 10.1111/j.1540-8159.2010.02887.x - DOI - PubMed
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

