Internal strain drives spontaneous periodic buckling in collagen and regulates remodeling

Abstract

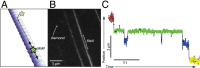
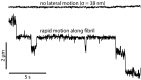
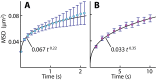
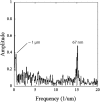
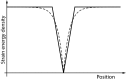
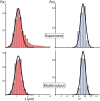
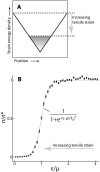
Fibrillar collagen, an essential structural component of the extracellular matrix, is remarkably resistant to proteolysis, requiring specialized matrix metalloproteinases (MMPs) to initiate its remodeling. In the context of native fibrils, remodeling is poorly understood; MMPs have limited access to cleavage sites and are inhibited by tension on the fibril. Here, single-molecule recordings of fluorescently labeled MMPs reveal cleavage-vulnerable binding regions arrayed periodically at ∼1-µm intervals along collagen fibrils. Binding regions remain periodic even as they migrate on the fibril, indicating a collective process of thermally activated and self-healing defect formation. An internal strain relief model involving reversible structural rearrangements quantitatively reproduces the observed spatial patterning and fluctuations of defects and provides a mechanism for tension-dependent stabilization of fibrillar collagen. This work identifies internal-strain-driven defects that may have general and widespread regulatory functions in self-assembled biological filaments.

Keywords: collagenase; matrix metalloproteinase; mechanosensing; pattern formation; single molecule.

Fig. 1.

Single-molecule tracking of MMP on fibrillar collagen. (A) Cartoon of experimental geometry (not to scale) depicting collagen fibril with 67-nm periodic axial banding (D period). Collagen remodeling enzymes (MMPs) (green star) bind and diffuse on the fibril. (B) Experimental geometry used for single-molecule enzyme tracking. Type I rat tail collagen fibrils were bound to a quartz slide and fluorescently labeled MMPs were visualized with TIRF microscopy. A fluorescent nanodiamond was used to correct for stage drift. (C) Example single-molecule trajectory depicting the position of the MMP along the collagen fibril as a function of time. As the MMP moves along the fibril, it dwells in well-separated binding regions, which are indicated by different colors. The spatial extent of the dwells (∼0.25 µm, full width at half maximum) exceeds the tracking uncertainty (∼40 nm at 10-ms exposure).

Fig. S1.

Single-molecule MMP trajectory of Fig. 1 plotted in both spatial dimensions. The enzyme is restricted to a narrow track in the longitudinal direction and maintains a stable lateral position (top). Note the much larger deviations in position as a result of longitudinal motion (bottom). Motion is apparent in the binding regions where the enzyme dwells (shown in different colors in Fig. 1). The SD of the lateral position provides an estimate for the measurement uncertainty: $\sigma =38$ nm for this particular trajectory at the collection rate of 85 frames per second. In the average of 1,188 dwell events, $\sigma =38\pm 8$ nm in the lateral direction and $105\pm 41$ nm longitudinally.

Fig. S2.

Average MSD curves for (A) single-molecule motion of MMP within binding regions, where the enzyme dwells, and (B) motion of binding region locations of Fig. 4B. MSD curves were calculated independently for each of the 10 sequential video recordings and then averaged; error bars are the SEM and reflect variations among the 10 repeated measurements. For visual clarity, only every tenth measurement point is plotted in A. The data in A and B are each well fit by the indicated subdiffusive power laws (black curves).

Fig. 2.

Mapping of collagen fibril binding locations from individual MMP trajectories. (A) Plot of MMP positions along the fibril as a function of time for hundreds of single molecules. Each continuous colored line corresponds to the trajectory of a single MMP. Long trajectories are colored more brightly. Colors are repeated for different molecules. (B) MMP binding data from the boxed region of A. (C) Histogram of binding positions from B over a sliding 1-s window updated every 0.2 s. (D) Location of MMP binding regions determined from the positions of peaks in C. Error bars equal to the SEM determined by Gaussian fitting are similar to the point size. Additional details are provided in Supporting Information.

Fig. 3.

Micrometer-scale periodicity of binding sites observed with different MMP constructs and different fibrils subjected to treatments to remove bound proteins: (A and B) active wild-type MMP-1, the prototypical collagenase; (C and D) active wild-type MMP-1 after washing with 1 M NaCl to remove nonspecifically bound proteins; (E and F) active wild-type MMP-9, a gelatinase; (G and H) mutant MMP-1 (E219Q) after 90 min of digestion with active MMP-1; and (I and J) active wild-type MMP-1 after 90 min of trypsin digestion, which degrades noncollagen proteins bound to the fibril. The periodicity is similar under all conditions. A, C, E, G, and I are spatiotemporal maps of binding regions similar to Figs. 2D and 4A. B, D, F, H, and J are histograms of the distances between adjacent binding regions at each time step (0.2 s) for the spatiotemporal maps in A, C, E, G, and I.

Fig. 4.

Binding regions in fibrillar collagen are periodic and dynamic. (A) Spatiotemporal map of collagen binding sites as calculated in Fig. 2D. Positions of individual binding regions persist over several tens of seconds with rough spatial periodicity. However, the sites move locally, and the number of binding sites changes occasionally through spontaneous creation (split) and annihilation (merge) events. (B) Map of binding site locations from more than 30,000 single-molecule trajectories plotted as a function of time. Positions along the fibril were measured with reference to the stable diamond fiducial marker. Gaps in the data set indicate breaks in the recording when enzyme was replenished in the sample chamber. (C) Single-molecule localization of binding events. Each point marks the mean position in two dimensions of an individual MMP molecule dwelling in a binding region for more than 0.2 s. Colors correspond to single-enzyme events in the first (red) and last (blue) portions in the data set in B and are darker where points overlap. The scale across the fibril is 3× the scale along the fibril. (D) Single-molecule localization of binding events over the full data set. (E) Correlation times of the periodic binding pattern fit with a sum of exponentials with decay times τ₁ = 1.4 ± 0.2 s and τ₂ = 18 ± 4 s (Supporting Information). (F) Histogram of the distances between adjacent binding regions at each time step (0.2 s) for the data in B. The peak indicating the dominant spatial periodicity of 1.12 ± 0.01 µm is also evident in the power spectral analysis of the binding patterns along the fibril (Inset and Supporting Information). (G) Detail of single-molecule localization from C for molecules that dwelled within a binding region for more than 1 s. Error bars are the SEM. The scale across the fibril is 3× the scale along the fibril axis.

Fig. 5.

Strain relief model recapitulates periodic and dynamic binding patterns in fibrillar collagen. (A) Buckles depicted as an alternate structural state in the fibril cartoon (top). The light pink shaded area between the dotted line (uniform strain energy density) and solid line (buckle strain energy density) is the strain energy relieved by formation of buckles. The distance over which the strain energy relief returns to the dotted line is the buckle width w, the distance between two buckles shown on the right is x, and the slope of the buckle strain energy density line is 2k. The area of the dark pink shaded triangle, [k(w – x)²/2], is the increase in energy associated with two buckles separated by a distance x < w. (B) The binding site separation probability distribution P(x) from Fig. 4F converted to an energy potential well through the relation, P(x) ∝ exp[−k(x – $\overline{x}$)²/(2k_BT)]. The energy was rescaled to zero at the center of the well. Filled data points were included in the fit of P(x) (Supporting Information), returning estimates for the spring constant, k = k_BT/σ² (effective stiffness of the potential well), the average buckle separation, $\overline{x}$ (the potential well center spacing), and buckling energy, µ = k$\overline{x}$²/2. (C) Monte Carlo simulations (Right) of the model using the fitted parameters resemble experimental data (Left).

Fig. S3.

Periodic positions of reduced modulus measured along the apex of a hydrated type I collagen fibril [modified with permission from ref. (Baldwin, et al.)]. The prominent peaks indicate that regions of lower molecular density occur at regular 67-nm axial intervals (as expected for the gap region of the D period) and also occur with a much longer, ∼1-µm axial period that is consistent with our data (compare with Figs. 3 and 4F).

Fig. S4.

Comparison of linear (solid curve) and nonlinear (dashed curve) strain energy relief profiles for isolated buckles. The two curves have equal areas of strain energy relief.

Fig. S5.

Comparison of experimental and simulation distributions of the spacing and number of buckles (MMP binding regions). Black curves are fits to $P\left(x\right)\propto \text{exp}[-{(x-\overline{x})}^2/\left(2{{\sigma }_x}^2\right)]$ and $P\left(n\right)\propto \text{exp}[-{(n-\overline{n})}^2/\left(2{{\sigma }_n}^2\right)]$, returning experimental values of $\overline{x}=1.12\pm 0.01$ µm, ${\sigma }_x=0.28\pm 0.01$ µm, $\overline{n}=9.48\pm 0.05$, and ${\sigma }_n=0.90\pm 0.05$ on L = 10.7 $\mathrm{\mu }\text{m}$ of fibril. The Monte Carlo method (with input parameters $k=12.3\hspace{0.17em}{k}_{B}T/\mathrm{\mu }{\text{m}}^2$, $\mathrm{\mu }=7.7\hspace{0.17em}{k}_{B}T$, and w = 5 µm) returns similar values: $\overline{x}=1.13\pm 0.03$ µm, ${\sigma }_x=0.29\pm 0.03$ µm, $\overline{n}=9.51\pm 0.01$, and ${\sigma }_n=0.80\pm \mathrm{0.01.}$

Fig. S6.

Strain relief model predicts buckling defects are removed by external tension. (A) Imposed tensile strain reduces the strain energy relieved per isolated buckle (shaded area). (B) Normalized density of buckles plotted as a function of the normalized strain energy relief per isolated buckle determined by Monte Carlo simulations with the same parameters used in Fig. S5. Error bars represent the SEM over 100 independently equilibrated buckle arrays. The transition from periodic bucking to no buckles occurs as the strain energy relief per isolated buckle, ε = kw²/2, is decreased, which corresponds to increasing levels of externally applied tensile strain. The transition midpoint is at the critical value, ε = µ, demonstrating a switch-like removal of buckle sites. For comparison, the gray curve is the two-state Boltzmann distribution 1/{1 + exp[−(ε − µ)/(k_BT)]}.