Optimal channels for channelized quadratic estimators

Abstract

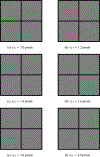
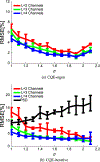
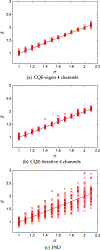
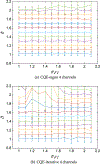
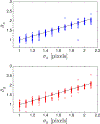
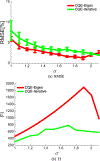
We present a new method for computing optimized channels for estimation tasks that is feasible for high-dimensional image data. Maximum-likelihood (ML) parameter estimates are challenging to compute from high-dimensional likelihoods. The dimensionality reduction from M measurements to L channels is a critical advantage of channelized quadratic estimators (CQEs), since estimating likelihood moments from channelized data requires smaller sample sizes and inverting a smaller covariance matrix is easier. The channelized likelihood is then used to form ML estimates of the parameter(s). In this work we choose an imaging example in which the second-order statistics of the image data depend upon the parameter of interest: the correlation length. Correlation lengths are used to approximate background textures in many imaging applications, and in these cases an estimate of the correlation length is useful for pre-whitening. In a simulation study we compare the estimation performance, as measured by the root-mean-squared error (RMSE), of correlation length estimates from CQE and power spectral density (PSD) distribution fitting. To abide by the assumptions of the PSD method we simulate an ergodic, isotropic, stationary, and zero-mean random process. These assumptions are not part of the CQE formalism. The CQE method assumes a Gaussian channelized likelihood that can be a valid for non-Gaussian image data, since the channel outputs are formed from weighted sums of the image elements. We have shown that, for three or more channels, the RMSE of CQE estimates of correlation length is lower than conventional PSD estimates. We also show that computing CQE by using a standard nonlinear optimization method produces channels that yield RMSE within 2% of the analytic optimum. CQE estimates of anisotropic correlation length estimation are reported to demonstrate this technique on a two-parameter estimation problem.

Fig. 1.

From top left to lower right, each 50 × 50 pixel image is a sample from a zero-mean, stationary, and isotropic Gaussian image ensemble. Twelve images are generated at correlation lengths from 1 to 2.1 pixels in 0.1 increments.

Fig. 2.

Four channels (i.e., rows of T) for CQE-eigen (see Subsection 5.B) where the FI is evaluated at six different values of the correlation length. Each channel is an eigenvector of ${\mathbf{K}}^{-1}\dot{\mathbf{K}}$. A high-frequency pattern results from K⁻¹ and a low-frequency pattern from $\dot{\mathbf{K}}$. In this example the channels look very similar at different σ_FI values; at the longest correlation length the channels appear to have more low-frequency content. As shown in Fig. 6, the resulting CQE estimates do not depend heavily on σ_FI except at the edge of the range of values, where the shortest correlation length channels are used to estimate the longest correlation lengths.

Fig. 3.

Four channels (i.e., rows of T) for CQE-iterative (see Subsection 6.C) where the FI is evaluated at six different values of the correlation length. These channels look different than CQE-eigen, although the trend of high-frequency content is still observable. As shown in Fig. 6, the resulting CQE estimates do not depend heavily on σ_FI except when short correlation length channels are used to estimate long correlation lengths.

Fig. 4.

RMSE of correlation length estimate versus the true value. Reported as mean RMSE and ±1 standard deviation calculated from five independent sets of 40 images. Different colors correspond to two, three, or four channels. Estimates from (a) CQE-eigen and (b) CQE-iterative are compared. The black line is the PSD estimator. CQE-eigen has lower RMSE than CQE-iterative. At three channels, this difference is within 2%. CQE-iterative performs better than PSD at three and four channels. For two channels the RMSE of PSD is lower than CQE-iterative at the smallest two correlation lengths.

Fig. 5.

Scatter plots of true versus estimated values for (a) CQE-eigen, (b) CQE-iterative, and (c) PSD. The true value of the correlation length is varied from 1 pixel to 2.1 pixels in 0.1 pixel increments. Forty images are generated at each correlation length using Eq. (32), and correlation length estimates are formed from each image and denoted by a red marker. The solid black line indicates equality between estimates and true values. All three estimators appear unbiased across the range of correlation lengths. The variance of CQE-eigen and CQE-iterative is close to invariant to the true value of the correlation length. Conversely, the variance of PSD increases as the correlation length increases.

Fig. 6.

Mean and standard deviation of (a) CQE-eigen and (b) CQE-iterative estimates at varying values of σ_FI, the parameter used in the FI channel maximization. Different colors correspond to estimates at different true values of the parameter. For CQE-eigen the mean value of the estimates does not vary more than 0.02 pixels with respect to σ_FI, except for the longest correlation length of 2.1 pixels. Here the mean varies by about 0.1 pixels. The estimation performance invariance to σ_FI is extremely helpful since, in practice, σ_FI is approximated from prior knowledge. For CQE-iterative, the variance of the estimates is greater and the mean value of the estimates varies more with respect to σ_FI. For small values of σ_FI (below 1.6 pixels) and long correlation lengths (above 1.6 pixels), the CQE-iterative bias is above 1.0. However, outside of this region CQE-iterative maintain invariance to σ_FI.

Fig. 7.

Four channels (i.e., rows of T) for CQE-eigen of multiple parameters (see Subsection 6.D) where the FI is evaluated at three different values of the correlation length. In the left column are channels to estimate σ_x and in the right column are channels to estimate σ_y.

Fig. 8.

Estimates of anisotropic correlation length using four CQE-eigen channels on 288 images. The RMSE is 8% in the x direction and 9% in the y direction. The increase in estimation task difficulty is apparent since, for CQE-eigen, the two-parameter RMSEs are almost double the one-parameter RMSE for the same number of channels. However, the CQE-eigen two-parameter RMSEs are lower than the one-parameter PSD RMSE, which was usually over 10%.

Fig. 9.

Comparison of CQE-eigen and CQE-iterative for isotropic correlation length estimation both with three channels. (a) RMSE mean and ±1 standard deviation from five independent sets of 40 images. The mean RMSE difference between the estimators is equal to or less than 2%. In (b), the FI (σ_FI = 1.5) of CQE-eigen grows linearly with correlation length until decreasing at 2.0 pixels. CQE-iterative increases more slowly with correlation length and begins decreasing at 1.9 pixels.