Protein-protein docking by fast generalized Fourier transforms on 5D rotational manifolds
- PMID: 27412858
- PMCID: PMC4968711
- DOI: 10.1073/pnas.1603929113
Protein-protein docking by fast generalized Fourier transforms on 5D rotational manifolds
Abstract
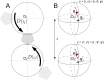
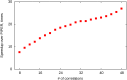
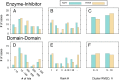
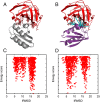
Energy evaluation using fast Fourier transforms (FFTs) enables sampling billions of putative complex structures and hence revolutionized rigid protein-protein docking. However, in current methods, efficient acceleration is achieved only in either the translational or the rotational subspace. Developing an efficient and accurate docking method that expands FFT-based sampling to five rotational coordinates is an extensively studied but still unsolved problem. The algorithm presented here retains the accuracy of earlier methods but yields at least 10-fold speedup. The improvement is due to two innovations. First, the search space is treated as the product manifold [Formula: see text], where [Formula: see text] is the rotation group representing the space of the rotating ligand, and [Formula: see text] is the space spanned by the two Euler angles that define the orientation of the vector from the center of the fixed receptor toward the center of the ligand. This representation enables the use of efficient FFT methods developed for [Formula: see text] Second, we select the centers of highly populated clusters of docked structures, rather than the lowest energy conformations, as predictions of the complex, and hence there is no need for very high accuracy in energy evaluation. Therefore, it is sufficient to use a limited number of spherical basis functions in the Fourier space, which increases the efficiency of sampling while retaining the accuracy of docking results. A major advantage of the method is that, in contrast to classical approaches, increasing the number of correlation function terms is computationally inexpensive, which enables using complex energy functions for scoring.
Keywords: FFT; manifold; protein docking.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

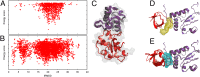
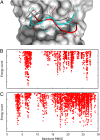
References
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

