Collective behavior as a driver of critical transitions in migratory populations
- PMID: 27429757
- PMCID: PMC4946155
- DOI: 10.1186/s40462-016-0083-8
Collective behavior as a driver of critical transitions in migratory populations
Abstract
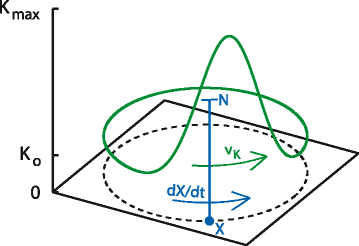
Background: Mass migrations are among the most striking examples of animal movement in the natural world. Such migrations are major drivers of ecosystem processes and strongly influence the survival and fecundity of individuals. For migratory animals, a formidable challenge is to find their way over long distances and through complex, dynamic environments. However, recent theoretical and empirical work suggests that by traveling in groups, individuals are able to overcome these challenges and increase their ability to navigate. Here we use models to explore the implications of collective navigation on migratory, and population, dynamics, for both breeding migrations (to-and-fro migrations between distinct, fixed, end-points) and feeding migrations (loop migrations that track favorable conditions).
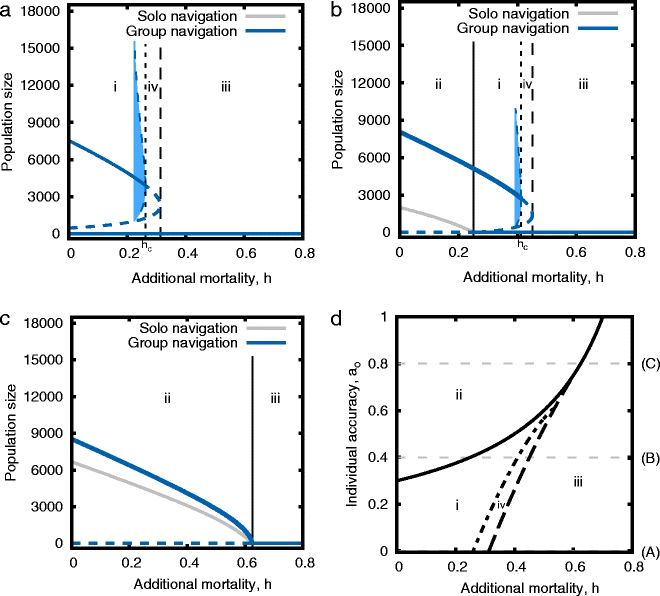
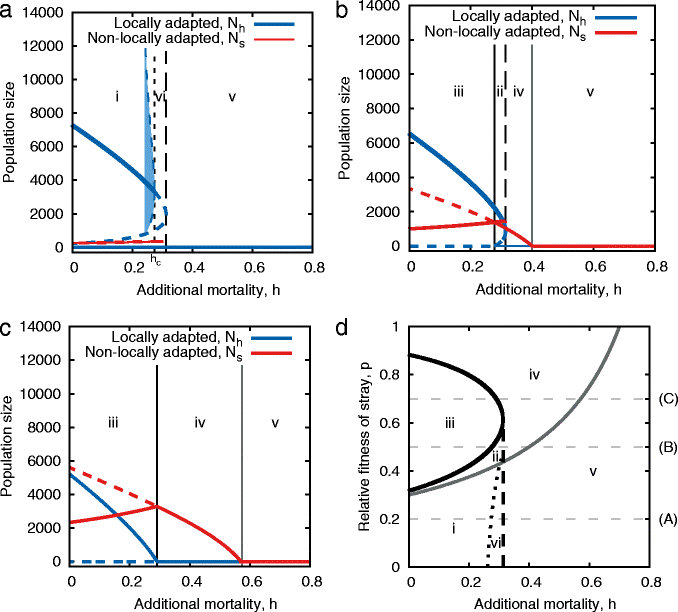
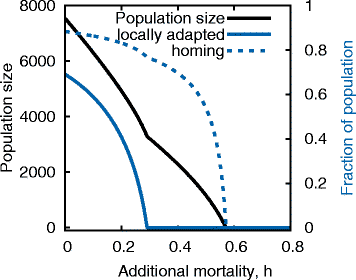
Results: We show that while collective navigation does improve a population's ability to migrate accurately, it can lead to Allee effects, causing the sudden collapse of populations if numbers fall below a critical threshold. In some scenarios, hysteresis prevents the migration from recovering even after the cause of the collapse has been removed. In collectively navigating populations that are locally adapted to specific breeding sites, a slight increase in mortality can cause a collapse of genetic population structure, rather than population size, making it more difficult to detect and prevent.
Conclusions: Despite the large interest in collective behavior and its ubiquity in many migratory species, there is a notable lack of studies considering the implications of social navigation on the ecological dynamics of migratory species. Here we highlight the potential for a previously overlooked Allee effect in socially migrating species that may be important for conservation and management of such species.
Keywords: Anadromous fish; Collective navigation; Dispersal; Local adaptation; Migration; Migratory birds; Migratory marine fish; Migratory ungulates; Population collapse.
Figures

References
-
- Doughty CE, Wolf A, Malhi Y. The legacy of the pleistocene megafauna extinctions on nutrient availability in amazonia. Nat Geosci. 2013;6(9):761–4. doi: 10.1038/ngeo1895. - DOI
-
- Estes RD. Gnu’s World: Serengeti Wildebeest Ecology and Life History. Oakland: University of California Press; 2014.
-
- Gould JL, Gould CG. Nature’s Compass: the Mystery of Animal Navigation. Princeton: Princeton University Press; 2012.
LinkOut - more resources
Full Text Sources
Other Literature Sources

