Energy and time determine scaling in biological and computer designs

Abstract

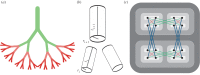
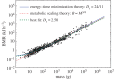
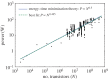
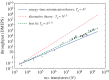
Metabolic rate in animals and power consumption in computers are analogous quantities that scale similarly with size. We analyse vascular systems of mammals and on-chip networks of microprocessors, where natural selection and human engineering, respectively, have produced systems that minimize both energy dissipation and delivery times. Using a simple network model that simultaneously minimizes energy and time, our analysis explains empirically observed trends in the scaling of metabolic rate in mammals and power consumption and performance in microprocessors across several orders of magnitude in size. Just as the evolutionary transitions from unicellular to multicellular animals in biology are associated with shifts in metabolic scaling, our model suggests that the scaling of power and performance will change as computer designs transition to decentralized multi-core and distributed cyber-physical systems. More generally, a single energy-time minimization principle may govern the design of many complex systems that process energy, materials and information.This article is part of the themed issue 'The major synthetic evolutionary transitions'.

Keywords: computer architecture; evolutionary transitions; metabolism; networks; scaling.

Figure 1.

Idealized branching models in biology (a) and computers (c). (a) A cardiovascular tree with branching factor λ = 2, H = 5 hierarchical branchings and N = 32 terminal branches at level 0 that represent capillaries. (b) The radius and length of successive branches: D_r defines the relative radius and D_l defines the relative length of pipe or wire between successive hierarchical levels (i and i + 1) in both biology (a) and computers (c). (c) The semi-hierarchical branching of logic wires on a computer chip. Each module within a hierarchical level is shaded the same colour. The purple, red, green and blue (thinnest to thickest) wires cross 0, 1, 2 and 3 modules, respectively. The wire lengths and widths increase as they cross more levels according to D_l and D_r. D_w defines the number of wires, determined by the ratio of internal (intra-module) communication per node to external (inter-module) communication per node. Here D_w = 2 so that a node is connected to all nodes within a module (in this case only 1) by a purple wire, 1/2 of the nodes in the next hierarchical level by red wires, 1/4 of the nodes in the next level by green wires, and 1/8 of the nodes in the next level by blue wires.

Figure 2.

The energy–time minimization model predicts metabolic scaling in mammals. Data from [23] show slight, but theoretically important, curvature in the scaling of metabolic rate versus mass of mammals. The theoretical optimum predicted by equation (3.8) with D_r = 24/11 is shown as a solid line. The West et al. 3/4 scaling prediction [5] is shown as a dotted line, and the best empirical fit of equation (3.8) to the data is shown as a dashed line (D_r = 2.50).

Figure 3.

The energy–time minimization model predicts power scaling in chips. Each data point represents a microprocessor chip, with active power and number of transistors per chip from [11]. The energy–time minimization model prediction (equation (3.12)) is shown as solid line, and the best-fit line is shown as dashed line.

Figure 4.

The energy–time minimization model predicts how throughput scales with the number of transistors. The raw data and their sources are included as electronic supplementary material. The model prediction (equation (3.13)) is shown as a solid line. The dotted line shows an alternative prediction if throughput were bound by the nodes (switching speed) rather than the network. The dashed line is the best fit to the data.