Host-Pathogen Coevolution and the Emergence of Broadly Neutralizing Antibodies in Chronic Infections

Abstract

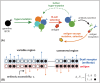
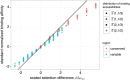
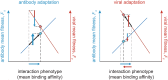
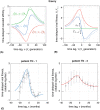
The vertebrate adaptive immune system provides a flexible and diverse set of molecules to neutralize pathogens. Yet, viruses such as HIV can cause chronic infections by evolving as quickly as the adaptive immune system, forming an evolutionary arms race. Here we introduce a mathematical framework to study the coevolutionary dynamics between antibodies and antigens within a host. We focus on changes in the binding interactions between the antibody and antigen populations, which result from the underlying stochastic evolution of genotype frequencies driven by mutation, selection, and drift. We identify the critical viral and immune parameters that determine the distribution of antibody-antigen binding affinities. We also identify definitive signatures of coevolution that measure the reciprocal response between antibodies and viruses, and we introduce experimentally measurable quantities that quantify the extent of adaptation during continual coevolution of the two opposing populations. Using this analytical framework, we infer rates of viral and immune adaptation based on time-shifted neutralization assays in two HIV-infected patients. Finally, we analyze competition between clonal lineages of antibodies and characterize the fate of a given lineage in terms of the state of the antibody and viral populations. In particular, we derive the conditions that favor the emergence of broadly neutralizing antibodies, which may have relevance to vaccine design against HIV.

Fig 1. coevolution of antibodies and viruses.

(A) Schematic of affinity maturation in a germinal center. A naive, germline B-cell receptor (black) with marginal binding affinity for the circulating antigen (red pentagon) enters the process of affinity maturation in a germinal center. Hypermutations produce a diverse set of B-cell receptors (colors), the majority of which do not increase the neutralization efficacy of B-cells, except for some beneficial mutations that increase binding affinity (dark blue and green) to the presented antigen. The selected B-cells may enter the blood and secrete antibodies, or enter further rounds of hypermutations to enhance their neutralization ability. Antigens mutate and are selected (yellow pentagon) based on their ability to escape the current immune challenge. (B) We model the interaction between the genotype of a B-cell receptor and its secreted antibody (blue) with a viral genotype (red) in both variable and conserved regions of the viral genome. The black and white circles indicate the state of the interacting loci with values ±1. Loci in the conserved region of the virus are fixed at +1. The length of the arrows indicate the contribution of each locus to the binding affinity, κ_i, which is a measure of the accessibility of an antibody lineage to viral epitopes. The blue arrows indicate the interactions that increase binding affinity (i.e., loci with same signs in antibody and viral genotype), whereas red arrows indicate interaction that decrease the affinity (i.e., loci with opposite signs in antibody and viral genotype.)

Fig 2. Effect of selection on immune-virus binding affinity.

The stationary mean binding affinity, rescaled by antibody binding diversity ($\mathcal{E}/\sqrt{M_{A,2}/4{\theta }_a}$), on the y-axis, is well approximated by the scaled selection difference between antibody and viral populations, Δs_av, as predicted by our analysis (eq (6)). Points show results of Wright-Fisher simulations, and the solid line has slope 1. Note that the mean binding affinity is insensitive to the details of heterogeneous binding accessibilities, κ_i, associated with an antibody lineage. Accessibilities κ_i are drawn from several different Γ-distributions, shown in legend. Small deviations from the predicted mean binding are caused by higher moments of binding affinities, which can also be understood analytically (S1 Fig). Simulation parameters are detailed in the Materials and Methods.

Fig 3. Fitness and transfer flux in antibody-viral coevolution.

The schematic diagram shows adaptation of antibody (blue diamond) and viral (red diamond) populations on their respective fitness landscapes, which depend on the common binding phenotype shown on the x-axis (i.e., the mean binding affinity). During one step of antibody adaptation (left), mean binding affinity increases (horizontal blue arrow) to enhance the fitness of the antibody population, with a rate equal to the antibody fitness flux ϕ_A (upward blue arrow). In the regime of strong selection, the fitness flux is proportional to the variance of fitness in the population; see eq (8). Adaptation of antibodies reduces the mean fitness in the viral population, with a rate proportional to the transfer flux from antibodies to viruses ${\mathcal{T}}_{A\to V}$ (downward red/blue arrow). On the other hand, viral adaptation (right) reduces the binding affinity and affects the fitness of both populations, with rates proportional to the viral fitness flux ϕ_V (upward red arrow) and the transfer flux from viruses to antibodies ${\mathcal{T}}_{V\to A}$ (downward blue/red arrow); see eq (9). Cumulative fitness flux (the sum of upward arrows) and cumulate transfer flux (the sum of downward arrows) over an evolutionary period quantify the amount of adaptation and interaction in the two antagonistic populations.

Fig 4. Time-shifted binding assays between antigens and antibodies provide a definitive signature of viral-immune coevolution.

Viruses perform best against antibodies from the past and perform worst against antibodies from the future due to the adaptation of antibodies. (A) Stationary rescaled binding affinity between viruses from time t and antibodies from time t + τ, averaged over all t: ε_τ = 〈∑_α,γ E_αγ y^γ(t)x^α(t + τ)〉_t/E₀, and (B) time-shifted mean fitness of viruses N_v F_V;τ = −s_v ε_τ, are shown for three regimes of coevolutionary dynamics: strong adaptation of both populations $s_a^2{\theta }_a\sim s_v^2{\theta }_v$, with s_a = s_v = 2 (blue), stronger adaptation of viruses $s_v^2{\theta }_v\gg s_a^2{\theta }_a$ with s_v = 2, s_a = 0 (red), and stronger adaptation of antibodies $s_a^2{\theta }_a\gg s_v^2{\theta }_v$ with s_v = 0, s_a = 2 (green). Wright-Fisher simulations (solid lines) are compared to the analytical predictions from eqs. (S102, S103) in S1 Text for each regime (dashed lines). The “S”-shape curve in the blue regime is a signature of two antagonistically coevolving populations s_v θ_v ∼ s_a θ_a. For large time-shifts, binding relaxes to its neutral value, zero, as mutations randomize genotypes. In the absence of selection in one population, the time-shifted binding affinity reflects adaptation of one population against stochastic variation in the other due to mutation and genetic drift. The slope of time-shifted fitness at lag τ = 0 is the viral population’s fitness flux (slope towards the past) and the transfer flux from the opposing population (slope towards the future), which are equal to each other in the stationary state. The slope of the dotted lines indicate the predicted fitness flux and transfer flux (eqs. (8 and 9)). Time-shifted fitness shown here does not include binding to the conserved region since that value is constant for all time-shifts in stationarity (see S6 Fig for non-stationary state). Simulation parameters are given in the Materials and Methods. (C) Empirical time-shifted fitness measurements of HIV based on a neutralization titer (IC₅₀) [11], averaged over all time points with equal time-shift τ. Circles show averaged fitness ± 1 standard error, and crosses show fitness at time-shifts with only a single data point. Solid lines show analytical fits of our model to the data (see Materials and Methods and Section F of S1 Text). In patient TN-1, viruses and antibodies experience a comparable adaptive pressure, with a similar time-shift pattern to the blue “S-curve” in panel (B). In patient TN-3, however, adaptation in viruses is much stronger than in antibodies, resulting in an imbalanced shape of the time-shifted fitness curve, similar to the red curve in panel (B).

Fig 5. Competition between antibody lineages, and fixation of broadly neutralizing antibodies.

(A) Simulation of competition between 20 clonal antibody lineages against a viral population. Lineages with higher mean fitness, higher fitness flux, and lower transfer flux tend to dominate the antibody repertoire. Each color represents a distinct antibody lineage, however there is also diversity within each lineage from somatic hypermutations. The reduction in the number of circulating lineages resembles the reduction in the number of active B-cell clones within the life-time of a germinal center [8]. Lineages are initialized as 500 random sequences with random accessibilities ${\kappa }^{\mathcal{C}}$’s, unique to each lineage, drawn from an exponential distribution with rate parameter 3. Total population sizes are N_a = N_v = 10⁴. Other simulation parameters are as specified in the Materials and Methods. (B) Analytical estimates of the fixation probability P_fix of a new antibody lineage, based on the state of the populations at the time of its introduction, compared to Wright-Fisher simulations (points) with two competing antibody lineages. A novel BnAb (blue) or non-BnAb (red) lineage is introduced at frequency 10% into a non-BnAb resident population (simulation procedures described in the Materials and Methods). BnAb lineages have a higher chance of fixing, compared to non-BnAb antibodies, when the viral population is diverse, whereas both types of Abs have similar chances in the limit of low viral diversity. The solid line is the analytical estimate for P_fix given by eq. (S140) in S1 Text, which is valid when the rate of adaptation is similar in antibodies and viruses. The dashed line is the analytical estimate for P_fix using the approximation in eq. (S141) in S1 Text, which is suitable when there is a strong imbalance between the two populations, as is the case for invasion of a BnAb with strong antibody selection s_a > 1 or against a viral population with low diversity. In the absence of selection (neutral regime), the fixation probability of an invading lineage is equal to its initial frequency of 10%. Panels show different strengths of antibody selection s_a = 0.5, 0.75, 1,2 against a common viral selection strength s_v = 1. Viral diversity is influenced mostly by the viral nucleotide diversity θ_v, which ranges from 0.002 to 0.1. Other simulation parameters are specified in the Materials and Methods.