The Moses-Littenberg meta-analytical method generates systematic differences in test accuracy compared to hierarchical meta-analytical models

Abstract

Objective: To compare meta-analyses of diagnostic test accuracy using the Moses-Littenberg summary receiver operating characteristic (SROC) approach with those of the hierarchical SROC (HSROC) model.

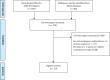
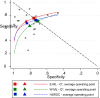
Study design and setting: Twenty-six data sets from existing test accuracy systematic reviews were reanalyzed with the Moses-Littenberg model, using equal weighting ("E-ML") and weighting by the inverse variance of the log DOR ("W-ML"), and with the HSROC model. The diagnostic odds ratios (DORs) were estimated and covariates added to both models to estimate relative DORs (RDORs) between subgroups. Models were compared by calculating the ratio of DORs, the ratio of RDORs, and P-values for detecting asymmetry and effects of covariates on DOR.

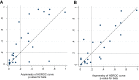
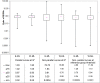
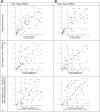
Results: Compared to the HSROC model, the Moses-Littenberg model DOR estimates were a median of 22% ("E-ML") and 47% ("W-ML") lower at Q*, and 7% and 42% lower at the central point in the data. Instances of the ML models giving estimates higher than the HSROC model also occurred. Investigations of heterogeneity also differed; the Moses-Littenberg models on average estimating smaller differences in RDOR.

Conclusions: Moses-Littenberg meta-analyses can generate lower estimates of test accuracy, and smaller differences in accuracy, compared to mathematically superior hierarchical models. This has implications for the usefulness of meta-analyses using this approach. We recommend meta-analysis of diagnostic test accuracy studies to be conducted using available hierarchical model-based approaches.

Keywords: Diagnostic odds ratio; Diagnostic test accuracy; Hierarchical models; Meta-analysis; Summary ROC curves; Systematic review.

Fig. 1

Flowchart of the review selection process. DARE, Database of Abstracts of Reviews of Effects.

Fig. 2

Comparison of diagnostic odds ratios: ML models vs. HSROC model. (A) Box and whisker plots of ratio of DORs between models (HSROC model estimate as reference). (B) Scatter plot of ratio of DORs between models (HSROC model estimate as reference). [ ] Denotes reference number for five reviews responsible for most of the extreme differences of DOR. DOR, diagnostic odds ratio; E-ML, equal-weight Moses–Littenberg; HSROC, hierarchical SROC; max, maximum ratio of DORs; mean threshold, point on the SROC curve near to the center of the data; min, minimum ratio of DORs; ML, Moses–Littenberg; p75, ratio of DORs at the 75th percentile; p50, ratio of DORs at the 50th percentile (median); p25, ratio of DORs at the 25th percentile; Q*, point on SROC curve where sensitivity = specificity; SROC, summary receiver operating characteristic; W-ML, Moses–Littenberg model weighted by inverse variance of D.

Fig. 3

Comparison of test of statistical significance of SROC curve asymmetry. (A) E-ML model vs. HSROC model. (B) W-ML model vs. HSROC model. HSROC, hierarchical SROC; E-ML, equal-weight Moses–Littenberg; SROC, summary receiver operating characteristic; W-ML, Moses–Littenberg model weighted by inverse variance of D.

Fig. 4

Ratio of relative DORs (RDORs) between models (HSROC model estimate as reference). DOR, diagnostic odds ratio; E-ML, equal-weight Moses–Littenberg; HSROC, hierarchical SROC; max, maximum ratio of DORs; min, minimum ratio of DORs; nonparallel curves, RDORs between study subgroups estimated allowing SROC curves to have different shapes (nonparallel); parallel curves, RDORs between study subgroups estimated assuming SROC curves have same shape (parallel); p75, ratio of DORs at the 75th percentile; p50, ratio of DORs at the 50th percentile (median); p25, ratio of DORs at the 25th percentile; Q*, point on SROC curve where sensitivity = specificity; RDOR, relative diagnostic odds ratio; reference group threshold, RDOR estimated at the point on the SROC curve near to the center of the data in the reference group; SROC, summary receiver operating characteristic; W-ML, Moses–Littenberg model weighted by inverse variance of D.

Fig. 5

Comparison of tests of statistical significance for difference in accuracy. E-ML, equal-weight Moses–Littenberg; HSROC, hierarchical SROC; Q*, point on SROC curve where sensitivity = specificity; RDOR, relative diagnostic odds ratio; SROC, summary receiver operating characteristic; W-ML, Moses–Littenberg model weighted by inverse variance of D.