Optimizing Silicon Oxide Embedded Silicon Nanocrystal Inter-particle Distances

Abstract

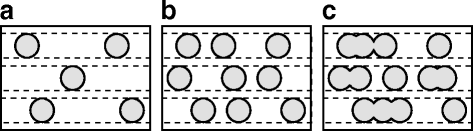
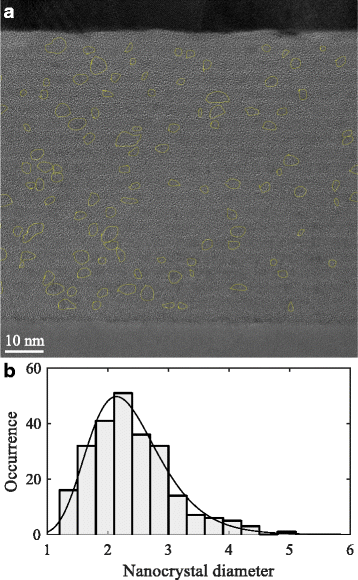
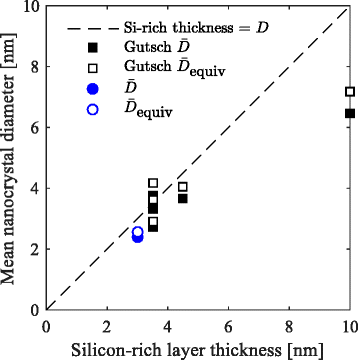
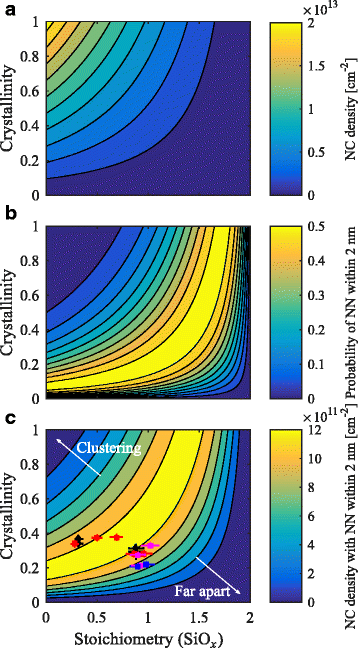
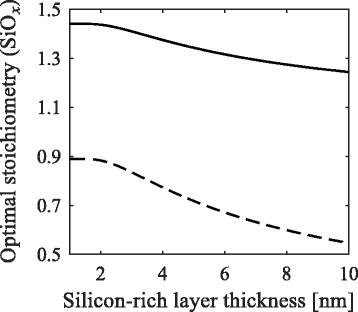
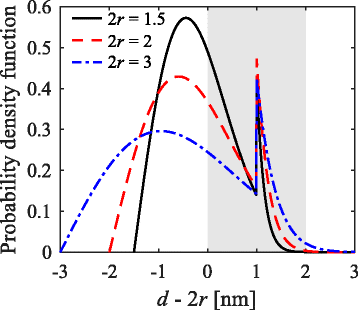
We demonstrate an analytical method to optimize the stoichiometry and thickness of multilayer silicon oxide films in order to achieve the highest density of non-touching and closely spaced silicon nanocrystals after annealing. The probability of a nanocrystal nearest-neighbor distance within a limited range is calculated using the stoichiometry of the as-deposited film and the crystallinity of the annealed film as input parameters. Multiplying this probability with the nanocrystal density results in the density of non-touching and closely spaced silicon nanocrystals. This method can be used to estimate the best as-deposited stoichiometry in order to achieve optimal nanocrystal density and spacing after a subsequent annealing step.

Keywords: Inter-particle distance; Silicon nanocrystal; Silicon oxide; Spacing; Stoichiometry.

Fig. 1

Nanocrystal spacing and clustering. Nanocrystals formed in silicon-rich layers with relatively low (a), medium (b), and high (c) excess silicon, separated by stoichiometric buffer layers

Fig. 2

Nanocrystals in a multilayer structure shown schematically. Nanocrystals in a multilayer structure shown schematically, including the nanocrystal radius r, buffer layer thickness t, and inter-particle distance d. The enclosing box around a nanocrystal is shown for the right-hand nanocrystal

Fig. 3

TEM image of a multilayer sample and its nanocrystal diameter histogram. a Cross-sectional high-resolution TEM image of an annealed multilayer sample with silicon-rich and buffer layer thicknesses of 3 and 1 nm, respectively. b The histogram of the sample’s nanocrystal diameters. Approximately 250 nanocrystals were measured. The histogram is fitted with a log-normal probability density function with μ= 0.83 nm and σ= 0.27 nm

Fig. 4

Nanocrystal diameter in a multilayer sample as a function of the silicon-rich layer thickness. The mean nanocrystal diameter $\overline{D}$ (solid symbols) and the mean equivalent diameter ${\overline{D}}_{\text{equiv}}$ (open symbols) for samples with varying silicon-rich layer thicknesses. The black data points are obtained from Gutsch et al. [18]. The dashed line represents the equality between the nanocrystal diameter and the silicon-rich layer thickness

Fig. 5

Nanocrystal density, NN probability, and NN density. The 2D nanocrystal (NC) density (a), the probability of finding a nearest neighbor (NN) within 2 nm (b), and the density of nanocrystals with a NN within 2 nm (c) as a function of the silicon-rich layer composition and crystallinity for a sample with silicon-rich and buffer layer thicknesses of 3 and 1 nm, respectively. The black diamonds represent tube furnace annealed intrinsic samples. The red, magenta, and blue squares show intrinsic, p-type and n-type samples annealed using RTA

Fig. 6

Optimal stoichiometry. The optimal stoichiometry for films with varying silicon-rich layer thicknesses for a sample with crystallinity of 1 (solid line) and 0.4 (dashed line). The buffer layer thickness is kept constant at 1 nm

Fig. 7

Nearest-neighbor distance probability density functions. The nearest-neighbor distance probability density functions for samples with silicon-rich layer thicknesses of 1.5, 2, and 3 nm and buffer layer thickness of 1 nm, calculated using their respective optimal compositions. The gray area depicts the range of desired nearest-neighbor distances. Shorter distances imply clustering, and greater distances lead to an insufficient tunneling probability