Using cell deformation and motion to predict forces and collective behavior in morphogenesis

Abstract

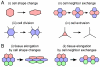
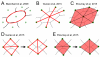
In multi-cellular organisms, morphogenesis translates processes at the cellular scale into tissue deformation at the scale of organs and organisms. To understand how biochemical signaling regulates tissue form and function, we must understand the mechanical forces that shape cells and tissues. Recent progress in developing mechanical models for tissues has led to quantitative predictions for how cell shape changes and polarized cell motility generate forces and collective behavior on the tissue scale. In particular, much insight has been gained by thinking about biological tissues as physical materials composed of cells. Here we review these advances and discuss how they might help shape future experiments in developmental biology.

Keywords: Collective motion; Deformation; Epithelium; Jamming; Morphogenesis; Tissue mechanics.

Figure 1

(A) Cellular processes underlying large-scale tissue deformation. (B) Large-scale elongation of a piece of tissue could be accounted for by (i) cell shape changes or (ii) cell neighbor exchanges.

Figure 2

Different methods to quantify cellular contributions to large-scale tissue deformation use different ways to measure cell shape. (A) Blanchard et al. fit the cell outline to an ellipse (red). Aspect ratio and angle of the ellipse are then used to characterize cell shape. (B) Guirao et al. define cell shape based on the connection lines (red) between neighboring cell centers (green dots). (C) Etournay et al. characterize cell shape based on triangles (red) whose corners are three neighboring cell centers (green dots). (D,E) Guirao et al. and Etournay et al. account for cell neighbor exchanges by addition and removal of either cell center connection lines or triangles, respectively. In all panels, gray lines represent cell-cell interfaces, green dots are cell centers, and the structures used to quantify cell shape are shown in red, respectively.

Figure 3

Cellular contributions to the convergence-extension-like deformation of the Drosophila melanogaster wing between the developmental times of 15 and 32 hours after puparium formation (hAPF) [15]. All curves shown were quantified using the triangle method and are cumulated over time. The overall deformation of the wing is shown as a blue solid curve. Positive and negative deformation correspond to shape changes in the fly wing shown in the upper and lower inset, respectively. This overall deformation is the precise sum of the following cellular contributions: cell shape changes (green), cell neighbor exchanges (red), cell divisions (orange), cell extrusions (cyan), and collective effects (magenta).

Figure 4

(A) Schematic diagram for a particle model of cells, where cells are circles with radius R and the distance between the edges of the cells is the overlap δ. δ is defined to be positive when cells overlap and negative when they are not touching. (B) Interaction potential V (δ) for a typical particle model. V (δ) is positive and the particles repel when δ is large and positive and the particles overlap significantly. The particles attract in the region where V (δ) is negative. Cells do not change shape, but their interaction changes as the cell centers move. (C) Schematic diagram of a cellular potts model for cells, where each cell is composed of a group of squares on a grid. Cells change shape when squares switch identity between cells. (D) Schematic diagram of a vertex model for cells, where each cell is composed of a series of vertices (such as the point labeled in red) connected by edges (such as the one labeled in blue). Cells change shape when vertices move or edges are added or removed.

Figure 5

(A) Single cell trajectory from a model where the velocity v₀ = 10 is much larger than the rotational noise D_r = 1. (B) Trajectory from a model where the rotational noise D_r = 10 is much greater than the velocity v₀ = 1. (C) Snapshot of motility-induced phase separation in a particle simulation with repulsive-only interactions and periodic boundaries, when v₀ = 50 and D_r = 1. (D,E) Cell polarization directions in simulations of a model (D) in a parameter regime where there is no collective motion or flocking and cell polarization directions are random, and (E) in a flocking regime where all cell polarization directions are strongly correlated.