The aerodynamics and control of free flight manoeuvres in Drosophila

Abstract

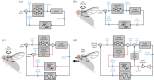
A firm understanding of how fruit flies hover has emerged over the past two decades, and recent work has focused on the aerodynamic, biomechanical and neurobiological mechanisms that enable them to manoeuvre and resist perturbations. In this review, we describe how flies manipulate wing movement to control their body motion during active manoeuvres, and how these actions are regulated by sensory feedback. We also discuss how the application of control theory is providing new insight into the logic and structure of the circuitry that underlies flight stability.This article is part of the themed issue 'Moving in a moving medium: new perspectives on flight'.

Keywords: Drosophila; aerodynamics; control theory; flight; insects.

Figure 1.

Kinematics and aerodynamics of fruit flies. (a) According to the helicopter model, a fly controls flight by modulating the magnitude of the wingbeat-average aerodynamic force and rotating its body around the roll, pitch and yaw axes. The required force and torque modulations are controlled by adjusting wing kinematics, which can be described by three Euler angles in the stroke plane reference frame: stroke angle, deviation angle and wing rotation angle. (b) Wingtip path and wing rotation angle (lollypop symbols), wing velocities (blue vectors) and instantaneous aerodynamic forces (orange vectors) at 25 equally spaced points in time throughout the wingbeat of a hovering fly (wingbeat frequency is 189 Hz) [27]. (c) Time history of wing Euler angles during steady flight. (d) Time history of vertical aerodynamic force. The light grey trace shows results from a quasi-steady aerodynamic model based on translational forces only; the dark grey trace is from a quasi-steady model that includes both translational and rotational forces [28]. The black trace shows the vertical force from a robotic fly experiment [27] and thus also includes unsteady aerodynamic effects such as wake capture and added mass forces. (e) Aerodynamic forces produced by a revolving robotic Drosophila wing model for a variable angle of attack [29]. The total force coefficient (C_F) is the resultant of the lift and drag components (C_L and C_D, respectively), and is oriented roughly perpendicular to the wing. All force coefficients are normalized by wing surface area and dynamic pressure. The ratio between C_L and C_D provides the lift-to-drag ratio L/D (black). (f) The flow field around a wing section (at 56% span) of a robotic Drosophila wing model moving at wing velocity U, measured using stereoscopic particle image velocimetry (PIV). Arrows indicate instantaneous in-plane fluid velocity, iso-lines show out-of-plane flow velocity in centimetres per second (positive indicates flow towards wingtip), and colour indicates fluid vorticity. The blue patch of high clockwise vorticity is the leading edge vortex (LEV), which enhances aerodynamic force production. Adapted from [30].

Figure 2.

Body saccade and escape manoeuvre. (a) Photomontage from a high-speed video of a fly performing a saccadic turn adapted from [53]. (b) Photomontage of evasive manoeuvre elicited by looming visual stimulus adapted from [27]. In both (a,b), the fly changes course by approximately 90°. The instantaneous flight velocity (blue vectors) and the horizontal component of the aerodynamic force produced by the fly (orange vectors) are overlaid on each fly image. (c) Time course of the total aerodynamic force and body torques produced throughout the saccadic turn shown in (a). (d) Equivalent data for the escape manoeuvre shown in (b). Forces are normalized by body mass (mg) and torques are normalized by the product of body mass and wing length (mg l). (e) Torque vectors for the bank (dark grey) and counter-bank phases (light grey) of 44 body saccades, adapted from [53]. The length of each vector depicts normalized torque magnitude. The black dashed vectors depict the averages for all manoeuvres. (f) Vectors indicating magnitude and orientation of body rotation during the bank phase of 92 evasive manoeuvres, adapted from [27]. The colour of each vector indicates the position of the looming stimulus that elicited each trail.

Figure 3.

Drosophila adjust wing kinematics to control total force, pitch torque, roll torque and yaw torque, adapted from [27,53]. In all top schematic panels, the net wingbeat-average forces and torques acting on the fruit fly are shown (not to scale). The second row shows the time history of wing movements and forces on the wings, whereby crosses define the wing hinge location for each half stroke, and serve as 10° reference scales for stroke and deviation angles. The third row shows the Euler angles as defined by figure 1a, and the bottom panels show the corresponding normalized forces or torques. (a) Forces and wing kinematics for a steady hovering fly (grey data) and for a fly that generates an increased flight force (green/black data). The corresponding wingbeat frequencies were 189 Hz and 230 Hz, respectively. (b) Comparison of the wing kinematics, forces and torques throughout a wingbeat that generates pitch down torque (orange data and grey lollypops), pitch up torque (blue data and black lollypops) and zero pitch torque (grey data in time-series plots). The changes in kinematics result in a shift in the position of the stroke-averaged centre of pressure, as illustrated in the top cartoon. (c) Wing kinematics, forces and torques of a fly producing roll torque. Upward rotating wing is indicated by black lollypops and blue data; downward rotating wing is indicated by grey lollypops and red data. The bottom panel shows roll torque throughout steady (grey) and roll-generating (black) wingbeat. (d) Wing kinematics, forces and torques of a fly producing yaw torque. Forward rotating wing is indicated by grey lollypops and red data, backwards rotating wing is indicated by black lollypops and blue data. The bottom panel shows yaw torque throughout the steady (grey) and yaw-generating (black) wingbeat.

Figure 4.

Control theory models of flight stabilization reflexes in Drosophila. (a) General from of simple proportional, integral and derivative (PID) feedback controller. In this and all other panels, delays are only indicated for the sensor block, although in actual systems they might occur throughout the feedback loop. (b) A simple PI controller for yaw velocity, based on [68]. (c) Another model of yaw stabilization that incorporates both visual and haltere feedback, based on results of [84,90]. The embedded loop using short-delay haltere feedback (red traces) acts to stabilize the outer loop using long-delay visual feedback. The haltere loop increases the stability of the vision loop by adding damping to the body dynamics. (d) A model for speed control based on [91]. As in yaw velocity controller shown in (c), a long-delay visual feedback loop is stabilized through the action of a short-delay mechanosensory loop (red traces), in this case mediated by the antennae. In this model, the action of the antennal loop in augmenting the passive damping of the system (indicated by ‘air drag’) is shown explicitly.