Is realistic neuronal modeling realistic?

Abstract

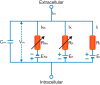
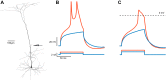
Scientific models are abstractions that aim to explain natural phenomena. A successful model shows how a complex phenomenon arises from relatively simple principles while preserving major physical or biological rules and predicting novel experiments. A model should not be a facsimile of reality; it is an aid for understanding it. Contrary to this basic premise, with the 21st century has come a surge in computational efforts to model biological processes in great detail. Here we discuss the oxymoronic, realistic modeling of single neurons. This rapidly advancing field is driven by the discovery that some neurons don't merely sum their inputs and fire if the sum exceeds some threshold. Thus researchers have asked what are the computational abilities of single neurons and attempted to give answers using realistic models. We briefly review the state of the art of compartmental modeling highlighting recent progress and intrinsic flaws. We then attempt to address two fundamental questions. Practically, can we realistically model single neurons? Philosophically, should we realistically model single neurons? We use layer 5 neocortical pyramidal neurons as a test case to examine these issues. We subject three publically available models of layer 5 pyramidal neurons to three simple computational challenges. Based on their performance and a partial survey of published models, we conclude that current compartmental models are ad hoc, unrealistic models functioning poorly once they are stretched beyond the specific problems for which they were designed. We then attempt to plot possible paths for generating realistic single neuron models.

Keywords: cable theory; channel kinetics; compartmental model; dendrites; ion channel.

Fig. 1.

The parallel conductance circuit model of the squid giant axon. I_m, membrane current; V_m, membrane potential; I_Na, sodium current; R_Na, membrane resistance to sodium; I_K, potassium current; R_K, membrane resistance to potassium; I_l, leak current; R_l, nonspecific membrane resistance.

Fig. 2.

A simple compartmental model. A: a schematic drawing of a neuron with a soma and one bifurcating dendrite. B: an equivalent circuit of the same neuron assuming only passive membrane parameters. C: an equivalent circuit of the same neuron assuming passive dendrites and an active soma. D: an equivalent circuit of the same neuron assuming that both soma and dendrites are excitable. R_m, membrane resistance.

Fig. 3.

Sampling parameter neighborhood in a parameter hypercube. We assume that parameter values in the model are uniformly distributed in an n-dimensional cube of unit length. We sample some portion of the total volume of the parameter space in a neighborhood around x̄. This neighborhood is a hypercube around x̄. It has volume V = lⁿ, and thus side length l = V^1/n. The range of variation for each parameter in the model is plotted as a function of the number of model parameters. The lines represent the range of parameter variation one needs to sample to properly sample the volume around a specific solution x̄. The lines were calculated for sampling of 10%, 1%, and 0.1% of the total volume around x̄.

Fig. 4.

Initiation of a proximal dendritic calcium spike by different models. A, C, and E: three models of layer 5 pyramidal neuron's somatic and dendritic voltage responses to simulated current injection by dendritic pipette 300 μm from soma. Current injection was 50 ms; 0.8 nA and 1.5 nA in A, 0.5 nA and 1 nA in C, 1 nA and 1.5 nA in E. Stimulation evoked forward propagation of action potentials toward the soma in all models. In all panels, the dendritic response is shown at the top and the somatic at the bottom. Color codes correspond to the level of current injected in each case. B, D, and F: the three model responses to simulated current injection by dendritic pipette at 300 μm from soma after eliminating the axon from the models. Curent injection was 50 ms; 1 nA and 1.5 nA in B, 1 nA and 1.5 nA in D, 2.5 nA and 3 nA in F. A local dendritic spike was evoked in both Hay model (D) and Almog model (F), whereas in Schaefer model only a small response was observed (B).

Fig. 5.

Initiation of a local dendritic regenerative potential at the proximal dendrite. A: reconstruction of a layer 5 pyramidal neuron stained with biocytin illustrating electrode placement. B: dendritic voltage responses to 50-ms current injection (0.8 and 1.1 nA) through the dendritic pipette at 300 μm, as illustrated in A. C: dendritic voltage responses to 50-ms current injection (1.6 and 1.8 nA) through the dendritic pipette at 300 μm when an application puffing pipette with an application solution (artificial cerebrospinal fluid and 10 μM tetrodotoxin) was placed on the axon initial segment, as illustrated in A. A local dendritic spike was evoked by a 1.8-nA current. Color codes correspond to the level of current injected in each case.

Fig. 6.

Regeneration of dendritic spike following partial block of voltage-gated calcium channels. A, C, and E: three layer 5 pyramidal neuron models' voltage response to distal injection (600 μm from the soma) of current with excitatory postsynaptic potential-like waveform (A: 1.8 nA, rising τ = 0.8 ms, declining τ = 4 ms; C: 1.5 nA, rising τ = 0.5 ms, declining τ = 5 ms; E: 1 nA, rising τ = 2 ms, declining τ = 10 ms). In each, current injection evoked a dendritic calcium spike, which forward propagated toward the soma and generated action potentials. In all panels, the dendritic response is shown at the top and the somatic at the bottom. Color codes correspond to the level of current injected in each case. Changing the permeability of the high-voltage-activated calcium channel (P_HVA) calcium channel conductivity to zero in all models reduced the amplitude and the shape of the calcium spike. However, larger injections of current (A: 3 nA, rising τ = 0.8 ms, declining τ = 4 ms; C: 2 nA, rising τ = 0.5 ms, declining τ = 5 ms; E: 1.35 nA, rising τ = 2 ms, declining τ = 10 ms) regenerated the dendritic calcium spike. B, D, and F: just as described above for A, C, and E, except it was the permeability of the medium-voltage activated calcium channel (P_MVA) that was changed to zero. It reduced the amplitude and the shape of the calcium spike only in the Hay and Almog models; in Schaefer model a subthreshold response was generated. Larger current injection (B: 4.7 nA, rising τ = 0.8 ms, declining τ = 4 ms; D: 2 nA, rising τ = 0.5 ms, declining τ = 5 ms; F: 1.2 nA, rising τ = 2 ms, declining τ = 10 ms) regenerated the dendritic calcium spike.

Fig. 7.

The refractory period of dendritic calcium spikes in different models. A paired depolarizing current of 50 ms with an increasing time interval (Δt = 50 ms) was injected to the distal apical dendrite (600 μm) of 3 different layer 5 pyramidal models (A: 1 nA; B: 0.6 nA; C: 1 nA). The somatic recording is depicted in cyan, and the dendritic one in red. A: Schaefer model reproduced a short refractory period of dendritic calcium spikes. B: Hay model reproduced a short refractory period of dendritic calcium spikes. C: Almog model reproduced a long refractory period of dendritic calcium spikes.

Fig. 8.

Interleaved interactions between components of automatic model optimization.